Integral tan(x) dx
A solução
You have entered
[src]
1 / | | tan(x) dx | / 0
$$\int\limits_{0}^{1} \tan{\left(x \right)}\, dx$$
Integral(tan(x), (x, 0, 1))
Detail solution
-
Rewrite the integrand:
-
Let .
Then let and substitute :
-
The integral of a constant times a function is the constant times the integral of the function:
-
The integral of is .
So, the result is:
-
Now substitute back in:
-
-
Add the constant of integration:
The answer is:
The answer (Indefinite)
[src]
/ | | tan(x) dx = C - log(cos(x)) | /
$$\int \tan{\left(x \right)}\, dx = C - \log{\left(\cos{\left(x \right)} \right)}$$
The graph
The answer
[src]
-log(cos(1))
$$- \log{\left(\cos{\left(1 \right)} \right)}$$
=
=
-log(cos(1))
$$- \log{\left(\cos{\left(1 \right)} \right)}$$
Gráfico
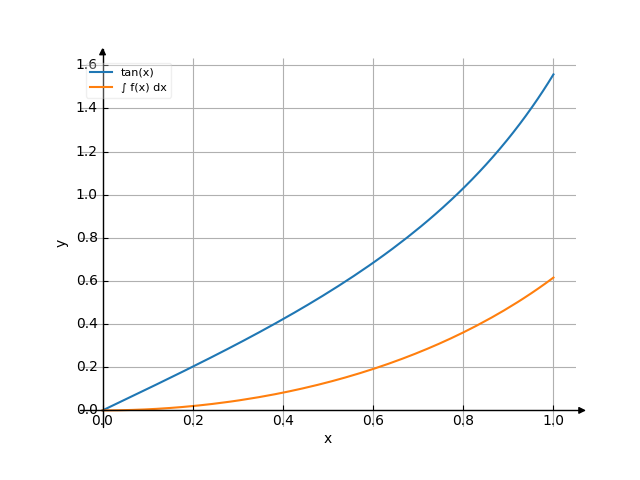
Estes exemplos também podem ser usados ao introduzir os limites superior e inferior de integração.

![Encontrar o integral de y = f(x) = tan(x) dx (tangente de (x)) - com solução detalhada [HÁ RESPOSTA!] tan(x)](/media/krcore-image-pods/176/hash/indefinite/7/d4/47e7aa67877ef57eaffb1d8b8c2b1.png)
 Integral 2x
Integral 2x
 Integral tg^2x
Integral tg^2x
 tan(x)
tan(x)
 tan(x)
tan(x)
 tan(x)
tan(x)