Mister Exam
Other calculators
- Graph of implicit function
- Derivative Step by Step
- Integral Step by Step
- Graph of parametric function
- Graph in Polar Coordinates
- Surface defined parametrically
- Surface defined by equation
- Curve in 3D space defined parametrically
- Area between lines
- The intersection points of functions
-
How to use it?
- Graphing y =:
-
2x^3
-
1/x^4
-
tan(x)
-
sqrt(3)sinx+cosx
- Derivative of:
-
tan(x)
- Limit of the function:
-
tan(x)
- Integral of d{x}:
-
tan(x)
-
Identical expressions
- tan(x)
- tangent of (x)
- tanx
-
Similar expressions
- 1/sqrt(tan(x^3-x))
- arctan(x/sqrt(1-x*x))
Graphing y = tan(x)
The solution
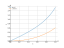
The graph of the function
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
$$\tan{\left(x \right)} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = 0$$
Numerical solution
$$x_{1} = -40.8407044966673$$
$$x_{2} = -62.8318530717959$$
$$x_{3} = 47.1238898038469$$
$$x_{4} = 75.398223686155$$
$$x_{5} = 12.5663706143592$$
$$x_{6} = -53.4070751110265$$
$$x_{7} = -75.398223686155$$
$$x_{8} = -47.1238898038469$$
$$x_{9} = -65.9734457253857$$
$$x_{10} = -59.6902604182061$$
$$x_{11} = -94.2477796076938$$
$$x_{12} = -18.8495559215388$$
$$x_{13} = -56.5486677646163$$
$$x_{14} = -81.6814089933346$$
$$x_{15} = 6.28318530717959$$
$$x_{16} = -15.707963267949$$
$$x_{17} = 56.5486677646163$$
$$x_{18} = 50.2654824574367$$
$$x_{19} = 78.5398163397448$$
$$x_{20} = -12.5663706143592$$
$$x_{21} = 72.2566310325652$$
$$x_{22} = 53.4070751110265$$
$$x_{23} = 15.707963267949$$
$$x_{24} = 62.8318530717959$$
$$x_{25} = 18.8495559215388$$
$$x_{26} = -37.6991118430775$$
$$x_{27} = -31.4159265358979$$
$$x_{28} = 37.6991118430775$$
$$x_{29} = 59.6902604182061$$
$$x_{30} = 0$$
$$x_{31} = -3.14159265358979$$
$$x_{32} = 69.1150383789755$$
$$x_{33} = -43.9822971502571$$
$$x_{34} = -91.106186954104$$
$$x_{35} = -28.2743338823081$$
$$x_{36} = -72.2566310325652$$
$$x_{37} = -34.5575191894877$$
$$x_{38} = -21.9911485751286$$
$$x_{39} = 28.2743338823081$$
$$x_{40} = 40.8407044966673$$
$$x_{41} = -9.42477796076938$$
$$x_{42} = 94.2477796076938$$
$$x_{43} = -6.28318530717959$$
$$x_{44} = 9.42477796076938$$
$$x_{45} = 21.9911485751286$$
$$x_{46} = 97.3893722612836$$
$$x_{47} = 81.6814089933346$$
$$x_{48} = -97.3893722612836$$
$$x_{49} = 43.9822971502571$$
$$x_{50} = 100.530964914873$$
$$x_{51} = 25.1327412287183$$
$$x_{52} = -84.8230016469244$$
$$x_{53} = -69.1150383789755$$
$$x_{54} = 91.106186954104$$
$$x_{55} = 3.14159265358979$$
$$x_{56} = -78.5398163397448$$
$$x_{57} = 84.8230016469244$$
$$x_{58} = 34.5575191894877$$
$$x_{59} = -25.1327412287183$$
$$x_{60} = -87.9645943005142$$
$$x_{61} = 65.9734457253857$$
$$x_{62} = -100.530964914873$$
$$x_{63} = -50.2654824574367$$
$$x_{64} = 87.9645943005142$$
$$x_{65} = 31.4159265358979$$
so we need to solve the equation:
$$\tan{\left(x \right)} = 0$$
Solve this equation
The points of intersection with the axis X:
Analytical solution
$$x_{1} = 0$$
Numerical solution
$$x_{1} = -40.8407044966673$$
$$x_{2} = -62.8318530717959$$
$$x_{3} = 47.1238898038469$$
$$x_{4} = 75.398223686155$$
$$x_{5} = 12.5663706143592$$
$$x_{6} = -53.4070751110265$$
$$x_{7} = -75.398223686155$$
$$x_{8} = -47.1238898038469$$
$$x_{9} = -65.9734457253857$$
$$x_{10} = -59.6902604182061$$
$$x_{11} = -94.2477796076938$$
$$x_{12} = -18.8495559215388$$
$$x_{13} = -56.5486677646163$$
$$x_{14} = -81.6814089933346$$
$$x_{15} = 6.28318530717959$$
$$x_{16} = -15.707963267949$$
$$x_{17} = 56.5486677646163$$
$$x_{18} = 50.2654824574367$$
$$x_{19} = 78.5398163397448$$
$$x_{20} = -12.5663706143592$$
$$x_{21} = 72.2566310325652$$
$$x_{22} = 53.4070751110265$$
$$x_{23} = 15.707963267949$$
$$x_{24} = 62.8318530717959$$
$$x_{25} = 18.8495559215388$$
$$x_{26} = -37.6991118430775$$
$$x_{27} = -31.4159265358979$$
$$x_{28} = 37.6991118430775$$
$$x_{29} = 59.6902604182061$$
$$x_{30} = 0$$
$$x_{31} = -3.14159265358979$$
$$x_{32} = 69.1150383789755$$
$$x_{33} = -43.9822971502571$$
$$x_{34} = -91.106186954104$$
$$x_{35} = -28.2743338823081$$
$$x_{36} = -72.2566310325652$$
$$x_{37} = -34.5575191894877$$
$$x_{38} = -21.9911485751286$$
$$x_{39} = 28.2743338823081$$
$$x_{40} = 40.8407044966673$$
$$x_{41} = -9.42477796076938$$
$$x_{42} = 94.2477796076938$$
$$x_{43} = -6.28318530717959$$
$$x_{44} = 9.42477796076938$$
$$x_{45} = 21.9911485751286$$
$$x_{46} = 97.3893722612836$$
$$x_{47} = 81.6814089933346$$
$$x_{48} = -97.3893722612836$$
$$x_{49} = 43.9822971502571$$
$$x_{50} = 100.530964914873$$
$$x_{51} = 25.1327412287183$$
$$x_{52} = -84.8230016469244$$
$$x_{53} = -69.1150383789755$$
$$x_{54} = 91.106186954104$$
$$x_{55} = 3.14159265358979$$
$$x_{56} = -78.5398163397448$$
$$x_{57} = 84.8230016469244$$
$$x_{58} = 34.5575191894877$$
$$x_{59} = -25.1327412287183$$
$$x_{60} = -87.9645943005142$$
$$x_{61} = 65.9734457253857$$
$$x_{62} = -100.530964914873$$
$$x_{63} = -50.2654824574367$$
$$x_{64} = 87.9645943005142$$
$$x_{65} = 31.4159265358979$$
Extrema of the function
In order to find the extrema, we need to solve the equation
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\tan^{2}{\left(x \right)} + 1 = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\tan^{2}{\left(x \right)} + 1 = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$2 \left(\tan^{2}{\left(x \right)} + 1\right) \tan{\left(x \right)} = 0$$
Solve this equation
The roots of this equation
$$x_{1} = 0$$
Сonvexity and concavity intervals:
Let’s find the intervals where the function is convex or concave, for this look at the behaviour of the function at the inflection points:
Concave at the intervals
$$\left[0, \infty\right)$$
Convex at the intervals
$$\left(-\infty, 0\right]$$
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$2 \left(\tan^{2}{\left(x \right)} + 1\right) \tan{\left(x \right)} = 0$$
Solve this equation
The roots of this equation
$$x_{1} = 0$$
Сonvexity and concavity intervals:
Let’s find the intervals where the function is convex or concave, for this look at the behaviour of the function at the inflection points:
Concave at the intervals
$$\left[0, \infty\right)$$
Convex at the intervals
$$\left(-\infty, 0\right]$$
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
$$\lim_{x \to -\infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
Let's take the limit
so,
equation of the horizontal asymptote on the left:
$$y = \left\langle -\infty, \infty\right\rangle$$
$$\lim_{x \to \infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = \left\langle -\infty, \infty\right\rangle$$
$$\lim_{x \to -\infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
Let's take the limit
so,
equation of the horizontal asymptote on the left:
$$y = \left\langle -\infty, \infty\right\rangle$$
$$\lim_{x \to \infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = \left\langle -\infty, \infty\right\rangle$$
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of tan(x), divided by x at x->+oo and x ->-oo
$$\lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right) = \lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
Let's take the limit
so,
inclined asymptote equation on the left:
$$y = x \lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
$$\lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right) = \lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
Let's take the limit
so,
inclined asymptote equation on the right:
$$y = x \lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
$$\lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right) = \lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
Let's take the limit
so,
inclined asymptote equation on the left:
$$y = x \lim_{x \to -\infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
$$\lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right) = \lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
Let's take the limit
so,
inclined asymptote equation on the right:
$$y = x \lim_{x \to \infty}\left(\frac{\tan{\left(x \right)}}{x}\right)$$
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
$$\tan{\left(x \right)} = - \tan{\left(x \right)}$$
- No
$$\tan{\left(x \right)} = \tan{\left(x \right)}$$
- Yes
so, the function
is
odd
So, check:
$$\tan{\left(x \right)} = - \tan{\left(x \right)}$$
- No
$$\tan{\left(x \right)} = \tan{\left(x \right)}$$
- Yes
so, the function
is
odd
The graph