Mister Exam
Other calculators:
-
How to use it?
- Limit of the function:
-
Limit of tan(x)
-
Limit of 1/2
- Limit of cot(5*pi*x)*log(x)
-
Limit of log(-1+x)/cot(pi*x)
- Graphing y =:
-
tan(x)
- Derivative of:
-
tan(x)
- Integral of d{x}:
-
tan(x)
-
Identical expressions
- tan(x)
- tangent of (x)
- tanx
Limit of the function tan(x)
The solution
You have entered
[src]
lim tan(x) pi x->--+ 2
$$\lim_{x \to \frac{\pi}{2}^+} \tan{\left(x \right)}$$
Limit(tan(x), x, pi/2)
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
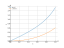
The graph
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to \frac{\pi}{2}^-} \tan{\left(x \right)} = -\infty$$
More at x→pi/2 from the left
$$\lim_{x \to \frac{\pi}{2}^+} \tan{\left(x \right)} = -\infty$$
$$\lim_{x \to \infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
More at x→oo
$$\lim_{x \to 0^-} \tan{\left(x \right)} = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+} \tan{\left(x \right)} = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-} \tan{\left(x \right)} = \tan{\left(1 \right)}$$
More at x→1 from the left
$$\lim_{x \to 1^+} \tan{\left(x \right)} = \tan{\left(1 \right)}$$
More at x→1 from the right
$$\lim_{x \to -\infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
More at x→-oo
More at x→pi/2 from the left
$$\lim_{x \to \frac{\pi}{2}^+} \tan{\left(x \right)} = -\infty$$
$$\lim_{x \to \infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
More at x→oo
$$\lim_{x \to 0^-} \tan{\left(x \right)} = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+} \tan{\left(x \right)} = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-} \tan{\left(x \right)} = \tan{\left(1 \right)}$$
More at x→1 from the left
$$\lim_{x \to 1^+} \tan{\left(x \right)} = \tan{\left(1 \right)}$$
More at x→1 from the right
$$\lim_{x \to -\infty} \tan{\left(x \right)} = \left\langle -\infty, \infty\right\rangle$$
More at x→-oo
One‐sided limits
[src]
lim tan(x) pi x->--+ 2
$$\lim_{x \to \frac{\pi}{2}^+} \tan{\left(x \right)}$$
-oo
$$-\infty$$
= -150.997792488028
lim tan(x) pi x->--- 2
$$\lim_{x \to \frac{\pi}{2}^-} \tan{\left(x \right)}$$
oo
$$\infty$$
= 150.997792488025
= 150.997792488025
The graph