Mister Exam
Other calculators
- Square Inequality Step-by-Step
- Inequality with the module Step by Step
- Logarithmic inequality online
-
How to use it?
- Inequation:
-
tg(x)>-(√3)/3
- log2^2*g>14log2*g−40.
- 1/(log(x-1)^(x/6))>=-1
- ctg(x)≥√3
- Derivative of:
-
tg(x)
- Graphing y =:
- tg(x)
- Integral of d{x}:
-
tg(x)
-
Identical expressions
- tg(x)>-(√ three)/ three
- tg(x) greater than minus (√3) divide by 3
- tg(x) greater than minus (√ three) divide by three
- tgx>-√3/3
- tg(x)>-(√3) divide by 3
-
Similar expressions
- tg(x)<=-√3/3
- tg(x)>+(√3)/3
- tg(p/3-2x)≥-√3/3
- tg(x/2+П/12)<=-sqrt(3)
- arctg(2x^2-5x-1)+arctg(x^2-2x+5)≤0
- tg(2x)<-√3/3
- tgx<=-sqrt3
tg(x)>-(√3)/3 inequation
The solution
You have entered
[src]
___
-\/ 3
tan(x) > -------
3
$$\tan{\left(x \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
tan(x) > -sqrt(3)/3
Detail solution
Given the inequality:
$$\tan{\left(x \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan{\left(x \right)} = \frac{\left(-1\right) \sqrt{3}}{3}$$
Solve:
Given the equation
$$\tan{\left(x \right)} = \frac{\left(-1\right) \sqrt{3}}{3}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = \pi n + \operatorname{atan}{\left(- \frac{\sqrt{3}}{3} \right)}$$
Or
$$x = \pi n - \frac{\pi}{6}$$
, where n - is a integer
$$x_{1} = \pi n - \frac{\pi}{6}$$
$$x_{1} = \pi n - \frac{\pi}{6}$$
This roots
$$x_{1} = \pi n - \frac{\pi}{6}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$\left(\pi n - \frac{\pi}{6}\right) - \frac{1}{10}$$
=
$$\pi n - \frac{\pi}{6} - \frac{1}{10}$$
substitute to the expression
$$\tan{\left(x \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
$$\tan{\left(\pi n - \frac{\pi}{6} - \frac{1}{10} \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
Then
$$x < \pi n - \frac{\pi}{6}$$
no execute
the solution of our inequality is:
$$x > \pi n - \frac{\pi}{6}$$
$$\tan{\left(x \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan{\left(x \right)} = \frac{\left(-1\right) \sqrt{3}}{3}$$
Solve:
Given the equation
$$\tan{\left(x \right)} = \frac{\left(-1\right) \sqrt{3}}{3}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x = \pi n + \operatorname{atan}{\left(- \frac{\sqrt{3}}{3} \right)}$$
Or
$$x = \pi n - \frac{\pi}{6}$$
, where n - is a integer
$$x_{1} = \pi n - \frac{\pi}{6}$$
$$x_{1} = \pi n - \frac{\pi}{6}$$
This roots
$$x_{1} = \pi n - \frac{\pi}{6}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$\left(\pi n - \frac{\pi}{6}\right) - \frac{1}{10}$$
=
$$\pi n - \frac{\pi}{6} - \frac{1}{10}$$
substitute to the expression
$$\tan{\left(x \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
$$\tan{\left(\pi n - \frac{\pi}{6} - \frac{1}{10} \right)} > \frac{\left(-1\right) \sqrt{3}}{3}$$
___
/1 pi\ -\/ 3
-tan|-- + --| > -------
\10 6 / 3
Then
$$x < \pi n - \frac{\pi}{6}$$
no execute
the solution of our inequality is:
$$x > \pi n - \frac{\pi}{6}$$
_____
/
-------ο-------
x_1
Solving inequality on a graph
Rapid solution
[src]
/ / pi\ /5*pi \\ Or|And|0 <= x, x < --|, And|---- < x, x < pi|| \ \ 2 / \ 6 //
$$\left(0 \leq x \wedge x < \frac{\pi}{2}\right) \vee \left(\frac{5 \pi}{6} < x \wedge x < \pi\right)$$
((0 <= x)∧(x < pi/2))∨((x < pi)∧(5*pi/6 < x))
Rapid solution 2
[src]
pi 5*pi
[0, --) U (----, pi)
2 6
$$x\ in\ \left[0, \frac{\pi}{2}\right) \cup \left(\frac{5 \pi}{6}, \pi\right)$$
x in Union(Interval.Ropen(0, pi/2), Interval.open(5*pi/6, pi))
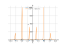
The graph