Integral of (2-x)dx dx
The solution
Detail solution
-
Let u=2−x.
Then let du=−dx and substitute −du:
-
The integral of a constant times a function is the constant times the integral of the function:
∫(−u)du=−∫udu
-
The integral of un is n+1un+1 when n=−1:
∫udu=2u2
So, the result is: −2u2
Now substitute u back in:
−2(2−x)2
-
Now simplify:
−2(x−2)2
-
Add the constant of integration:
−2(x−2)2+constant
The answer is:
−2(x−2)2+constant
The answer (Indefinite)
[src]
/ 2
| (2 - x)
| (2 - x)*1 dx = C - --------
| 2
/
2x−2x2
The graph
Use the examples entering the upper and lower limits of integration.
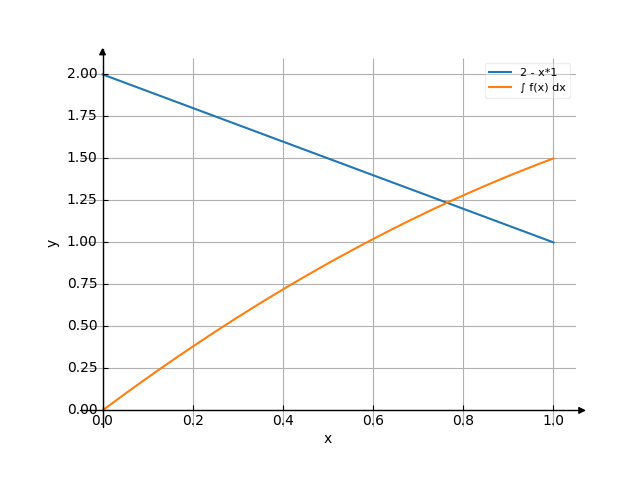

![Find the integral of y = f(x) = (2-x)dx ((2 minus x)dx) - with detailed solution [THERE'S THE ANSWER!] (2-x)dx](/media/krcore-image-pods/176/hash/indefinite/5/d9/ec76a92a0a12143ff768d7f126b57.png)
 Integral of (-1+u)/(1+u^2)
Integral of (-1+u)/(1+u^2)
 Integral of y^(-3)
Integral of y^(-3)
 Integral of x/(x^2+4)^(1/2)
Integral of x/(x^2+4)^(1/2)
 Integral of (x^5)e^(-x^2)
Integral of (x^5)e^(-x^2)