Mister Exam
Other calculators
- Square Inequality Step-by-Step
- Inequality with the module Step by Step
- Logarithmic inequality online
-
How to use it?
- Inequation:
- x^2+9p^2+2x+6y+2>=0
- 3x+1/5-1-2x/2>x
- (x-2)/(x-7)>0
- (x+40)/((x^3-16*x)*((x-4)/(3*x^2+11*x-4)-16/(16-x^2)))≤0
- Derivative of:
-
sin(t)
- Limit of the function:
-
sin(t)
- Integral of d{x}:
-
sin(t)
- Sum of series:
-
-0,6
-
Identical expressions
- sin(t)<- zero , six
- sinus of (t) less than minus 0,6
- sinus of (t) less than minus zero , six
- sint<-0,6
-
Similar expressions
- sin(t)<+0,6
- sint>=-1/2
- sint<1\3
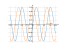
sin(t)<-0,6 inequation
The solution
Detail solution
Given the inequality:
$$\sin{\left(t \right)} < - \frac{3}{5}$$
To solve this inequality, we must first solve the corresponding equation:
$$\sin{\left(t \right)} = - \frac{3}{5}$$
Solve:
Given the equation
$$\sin{\left(t \right)} = - \frac{3}{5}$$
transform
$$\sin{\left(t \right)} + \frac{3}{5} = 0$$
$$\sin{\left(t \right)} + \frac{3}{5} = 0$$
Do replacement
$$w = \sin{\left(t \right)}$$
Move free summands (without w)
from left part to right part, we given:
$$w = - \frac{3}{5}$$
We get the answer: w = -3/5
do backward replacement
$$\sin{\left(t \right)} = w$$
substitute w:
$$x_{1} = -0.643501108793284$$
$$x_{2} = -19.493057030332$$
$$x_{3} = 66.6169468341789$$
$$x_{4} = 37.0556107342842$$
$$x_{5} = -15.0644621591557$$
$$x_{6} = -27.6308327735149$$
$$x_{7} = -107.457651330846$$
$$x_{8} = -94.8912807164871$$
$$x_{9} = 275.816652407109$$
$$x_{10} = 81.0379078845413$$
$$x_{11} = -13.2098717231525$$
$$x_{12} = 54.0505762198198$$
$$x_{13} = -63.4753541805892$$
$$x_{14} = 85.4665027557177$$
$$x_{15} = -40.197203387874$$
$$x_{16} = -46.4803886950536$$
$$x_{17} = -71.613129923772$$
$$x_{18} = -84.1795005381311$$
$$x_{19} = -33.9140180806944$$
$$x_{20} = -25.7762423375116$$
$$x_{21} = -50.90898356623$$
$$x_{22} = 91.7496880628973$$
$$x_{23} = 18.2060548127455$$
$$x_{24} = -101.174466023667$$
$$x_{25} = 16.3514643767422$$
$$x_{26} = 35.201020298281$$
$$x_{27} = 10.0682790695627$$
$$x_{28} = 87.3210931917209$$
$$x_{29} = 11.9228695055659$$
$$x_{30} = 139936.605069959$$
$$x_{31} = -8.7812768519761$$
$$x_{32} = -65.3299446165924$$
$$x_{33} = -77.8963152309515$$
$$x_{34} = -32.0594276446912$$
$$x_{35} = -59.0467593094128$$
$$x_{36} = -52.7635740022332$$
$$x_{37} = 93.6042784989005$$
$$x_{38} = 3280205.36115037$$
$$x_{39} = 60.3337615269994$$
$$x_{40} = -6.92668641597287$$
$$x_{41} = 79.1833174485381$$
$$x_{42} = -57.1921688734096$$
$$x_{43} = -2.49809154479651$$
$$x_{44} = 24.4892401199251$$
$$x_{45} = 30.7724254271046$$
$$x_{46} = 22.6346496839218$$
$$x_{47} = -38.3426129518708$$
$$x_{48} = 28.9178349911014$$
$$x_{49} = 68.4715372701822$$
$$x_{50} = -44.6257982590504$$
$$x_{51} = 98.0328733700769$$
$$x_{52} = -90.4626858453107$$
$$x_{53} = -21.3476474663353$$
$$x_{54} = -96.7458711524903$$
$$x_{55} = -76.0417247949483$$
$$x_{56} = 55.905166655823$$
$$x_{57} = 99.8874638060801$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{60} = 5.6396841983863$$
$$x_{61} = -88.6080954093075$$
$$x_{62} = 468.740806493672$$
$$x_{63} = 47.7673909126402$$
$$x_{64} = 62.1883519630026$$
$$x_{65} = 41.4842056054606$$
$$x_{66} = 49.6219813486434$$
$$x_{67} = -69.7585394877687$$
$$x_{68} = 43.3387960414638$$
$$x_{69} = -82.3249101021279$$
$$x_{70} = 3.78509376238308$$
$$x_{1} = -0.643501108793284$$
$$x_{2} = -19.493057030332$$
$$x_{3} = 66.6169468341789$$
$$x_{4} = 37.0556107342842$$
$$x_{5} = -15.0644621591557$$
$$x_{6} = -27.6308327735149$$
$$x_{7} = -107.457651330846$$
$$x_{8} = -94.8912807164871$$
$$x_{9} = 275.816652407109$$
$$x_{10} = 81.0379078845413$$
$$x_{11} = -13.2098717231525$$
$$x_{12} = 54.0505762198198$$
$$x_{13} = -63.4753541805892$$
$$x_{14} = 85.4665027557177$$
$$x_{15} = -40.197203387874$$
$$x_{16} = -46.4803886950536$$
$$x_{17} = -71.613129923772$$
$$x_{18} = -84.1795005381311$$
$$x_{19} = -33.9140180806944$$
$$x_{20} = -25.7762423375116$$
$$x_{21} = -50.90898356623$$
$$x_{22} = 91.7496880628973$$
$$x_{23} = 18.2060548127455$$
$$x_{24} = -101.174466023667$$
$$x_{25} = 16.3514643767422$$
$$x_{26} = 35.201020298281$$
$$x_{27} = 10.0682790695627$$
$$x_{28} = 87.3210931917209$$
$$x_{29} = 11.9228695055659$$
$$x_{30} = 139936.605069959$$
$$x_{31} = -8.7812768519761$$
$$x_{32} = -65.3299446165924$$
$$x_{33} = -77.8963152309515$$
$$x_{34} = -32.0594276446912$$
$$x_{35} = -59.0467593094128$$
$$x_{36} = -52.7635740022332$$
$$x_{37} = 93.6042784989005$$
$$x_{38} = 3280205.36115037$$
$$x_{39} = 60.3337615269994$$
$$x_{40} = -6.92668641597287$$
$$x_{41} = 79.1833174485381$$
$$x_{42} = -57.1921688734096$$
$$x_{43} = -2.49809154479651$$
$$x_{44} = 24.4892401199251$$
$$x_{45} = 30.7724254271046$$
$$x_{46} = 22.6346496839218$$
$$x_{47} = -38.3426129518708$$
$$x_{48} = 28.9178349911014$$
$$x_{49} = 68.4715372701822$$
$$x_{50} = -44.6257982590504$$
$$x_{51} = 98.0328733700769$$
$$x_{52} = -90.4626858453107$$
$$x_{53} = -21.3476474663353$$
$$x_{54} = -96.7458711524903$$
$$x_{55} = -76.0417247949483$$
$$x_{56} = 55.905166655823$$
$$x_{57} = 99.8874638060801$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{60} = 5.6396841983863$$
$$x_{61} = -88.6080954093075$$
$$x_{62} = 468.740806493672$$
$$x_{63} = 47.7673909126402$$
$$x_{64} = 62.1883519630026$$
$$x_{65} = 41.4842056054606$$
$$x_{66} = 49.6219813486434$$
$$x_{67} = -69.7585394877687$$
$$x_{68} = 43.3387960414638$$
$$x_{69} = -82.3249101021279$$
$$x_{70} = 3.78509376238308$$
This roots
$$x_{7} = -107.457651330846$$
$$x_{24} = -101.174466023667$$
$$x_{54} = -96.7458711524903$$
$$x_{8} = -94.8912807164871$$
$$x_{52} = -90.4626858453107$$
$$x_{61} = -88.6080954093075$$
$$x_{18} = -84.1795005381311$$
$$x_{69} = -82.3249101021279$$
$$x_{33} = -77.8963152309515$$
$$x_{55} = -76.0417247949483$$
$$x_{17} = -71.613129923772$$
$$x_{67} = -69.7585394877687$$
$$x_{32} = -65.3299446165924$$
$$x_{13} = -63.4753541805892$$
$$x_{35} = -59.0467593094128$$
$$x_{42} = -57.1921688734096$$
$$x_{36} = -52.7635740022332$$
$$x_{21} = -50.90898356623$$
$$x_{16} = -46.4803886950536$$
$$x_{50} = -44.6257982590504$$
$$x_{15} = -40.197203387874$$
$$x_{47} = -38.3426129518708$$
$$x_{19} = -33.9140180806944$$
$$x_{34} = -32.0594276446912$$
$$x_{6} = -27.6308327735149$$
$$x_{20} = -25.7762423375116$$
$$x_{53} = -21.3476474663353$$
$$x_{2} = -19.493057030332$$
$$x_{5} = -15.0644621591557$$
$$x_{11} = -13.2098717231525$$
$$x_{31} = -8.7812768519761$$
$$x_{40} = -6.92668641597287$$
$$x_{43} = -2.49809154479651$$
$$x_{1} = -0.643501108793284$$
$$x_{70} = 3.78509376238308$$
$$x_{60} = 5.6396841983863$$
$$x_{27} = 10.0682790695627$$
$$x_{29} = 11.9228695055659$$
$$x_{25} = 16.3514643767422$$
$$x_{23} = 18.2060548127455$$
$$x_{46} = 22.6346496839218$$
$$x_{44} = 24.4892401199251$$
$$x_{48} = 28.9178349911014$$
$$x_{45} = 30.7724254271046$$
$$x_{26} = 35.201020298281$$
$$x_{4} = 37.0556107342842$$
$$x_{65} = 41.4842056054606$$
$$x_{68} = 43.3387960414638$$
$$x_{63} = 47.7673909126402$$
$$x_{66} = 49.6219813486434$$
$$x_{12} = 54.0505762198198$$
$$x_{56} = 55.905166655823$$
$$x_{39} = 60.3337615269994$$
$$x_{64} = 62.1883519630026$$
$$x_{3} = 66.6169468341789$$
$$x_{49} = 68.4715372701822$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{41} = 79.1833174485381$$
$$x_{10} = 81.0379078845413$$
$$x_{14} = 85.4665027557177$$
$$x_{28} = 87.3210931917209$$
$$x_{22} = 91.7496880628973$$
$$x_{37} = 93.6042784989005$$
$$x_{51} = 98.0328733700769$$
$$x_{57} = 99.8874638060801$$
$$x_{9} = 275.816652407109$$
$$x_{62} = 468.740806493672$$
$$x_{30} = 139936.605069959$$
$$x_{38} = 3280205.36115037$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{7}$$
For example, let's take the point
$$x_{0} = x_{7} - \frac{1}{10}$$
=
$$-107.457651330846 + - \frac{1}{10}$$
=
$$-107.557651330846$$
substitute to the expression
$$\sin{\left(t \right)} < - \frac{3}{5}$$
$$\sin{\left(t \right)} < - \frac{3}{5}$$
Then
$$x < -107.457651330846$$
no execute
one of the solutions of our inequality is:
$$x > -107.457651330846 \wedge x < -101.174466023667$$
Other solutions will get with the changeover to the next point
etc.
The answer:
$$x > -107.457651330846 \wedge x < -101.174466023667$$
$$x > -96.7458711524903 \wedge x < -94.8912807164871$$
$$x > -90.4626858453107 \wedge x < -88.6080954093075$$
$$x > -84.1795005381311 \wedge x < -82.3249101021279$$
$$x > -77.8963152309515 \wedge x < -76.0417247949483$$
$$x > -71.613129923772 \wedge x < -69.7585394877687$$
$$x > -65.3299446165924 \wedge x < -63.4753541805892$$
$$x > -59.0467593094128 \wedge x < -57.1921688734096$$
$$x > -52.7635740022332 \wedge x < -50.90898356623$$
$$x > -46.4803886950536 \wedge x < -44.6257982590504$$
$$x > -40.197203387874 \wedge x < -38.3426129518708$$
$$x > -33.9140180806944 \wedge x < -32.0594276446912$$
$$x > -27.6308327735149 \wedge x < -25.7762423375116$$
$$x > -21.3476474663353 \wedge x < -19.493057030332$$
$$x > -15.0644621591557 \wedge x < -13.2098717231525$$
$$x > -8.7812768519761 \wedge x < -6.92668641597287$$
$$x > -2.49809154479651 \wedge x < -0.643501108793284$$
$$x > 3.78509376238308 \wedge x < 5.6396841983863$$
$$x > 10.0682790695627 \wedge x < 11.9228695055659$$
$$x > 16.3514643767422 \wedge x < 18.2060548127455$$
$$x > 22.6346496839218 \wedge x < 24.4892401199251$$
$$x > 28.9178349911014 \wedge x < 30.7724254271046$$
$$x > 35.201020298281 \wedge x < 37.0556107342842$$
$$x > 41.4842056054606 \wedge x < 43.3387960414638$$
$$x > 47.7673909126402 \wedge x < 49.6219813486434$$
$$x > 54.0505762198198 \wedge x < 55.905166655823$$
$$x > 60.3337615269994 \wedge x < 62.1883519630026$$
$$x > 66.6169468341789 \wedge x < 68.4715372701822$$
$$x > 72.9001321413585 \wedge x < 74.7547225773617$$
$$x > 79.1833174485381 \wedge x < 81.0379078845413$$
$$x > 85.4665027557177 \wedge x < 87.3210931917209$$
$$x > 91.7496880628973 \wedge x < 93.6042784989005$$
$$x > 98.0328733700769 \wedge x < 99.8874638060801$$
$$x > 275.816652407109 \wedge x < 468.740806493672$$
$$x > 139936.605069959 \wedge x < 3280205.36115037$$
$$\sin{\left(t \right)} < - \frac{3}{5}$$
To solve this inequality, we must first solve the corresponding equation:
$$\sin{\left(t \right)} = - \frac{3}{5}$$
Solve:
Given the equation
$$\sin{\left(t \right)} = - \frac{3}{5}$$
transform
$$\sin{\left(t \right)} + \frac{3}{5} = 0$$
$$\sin{\left(t \right)} + \frac{3}{5} = 0$$
Do replacement
$$w = \sin{\left(t \right)}$$
Move free summands (without w)
from left part to right part, we given:
$$w = - \frac{3}{5}$$
We get the answer: w = -3/5
do backward replacement
$$\sin{\left(t \right)} = w$$
substitute w:
$$x_{1} = -0.643501108793284$$
$$x_{2} = -19.493057030332$$
$$x_{3} = 66.6169468341789$$
$$x_{4} = 37.0556107342842$$
$$x_{5} = -15.0644621591557$$
$$x_{6} = -27.6308327735149$$
$$x_{7} = -107.457651330846$$
$$x_{8} = -94.8912807164871$$
$$x_{9} = 275.816652407109$$
$$x_{10} = 81.0379078845413$$
$$x_{11} = -13.2098717231525$$
$$x_{12} = 54.0505762198198$$
$$x_{13} = -63.4753541805892$$
$$x_{14} = 85.4665027557177$$
$$x_{15} = -40.197203387874$$
$$x_{16} = -46.4803886950536$$
$$x_{17} = -71.613129923772$$
$$x_{18} = -84.1795005381311$$
$$x_{19} = -33.9140180806944$$
$$x_{20} = -25.7762423375116$$
$$x_{21} = -50.90898356623$$
$$x_{22} = 91.7496880628973$$
$$x_{23} = 18.2060548127455$$
$$x_{24} = -101.174466023667$$
$$x_{25} = 16.3514643767422$$
$$x_{26} = 35.201020298281$$
$$x_{27} = 10.0682790695627$$
$$x_{28} = 87.3210931917209$$
$$x_{29} = 11.9228695055659$$
$$x_{30} = 139936.605069959$$
$$x_{31} = -8.7812768519761$$
$$x_{32} = -65.3299446165924$$
$$x_{33} = -77.8963152309515$$
$$x_{34} = -32.0594276446912$$
$$x_{35} = -59.0467593094128$$
$$x_{36} = -52.7635740022332$$
$$x_{37} = 93.6042784989005$$
$$x_{38} = 3280205.36115037$$
$$x_{39} = 60.3337615269994$$
$$x_{40} = -6.92668641597287$$
$$x_{41} = 79.1833174485381$$
$$x_{42} = -57.1921688734096$$
$$x_{43} = -2.49809154479651$$
$$x_{44} = 24.4892401199251$$
$$x_{45} = 30.7724254271046$$
$$x_{46} = 22.6346496839218$$
$$x_{47} = -38.3426129518708$$
$$x_{48} = 28.9178349911014$$
$$x_{49} = 68.4715372701822$$
$$x_{50} = -44.6257982590504$$
$$x_{51} = 98.0328733700769$$
$$x_{52} = -90.4626858453107$$
$$x_{53} = -21.3476474663353$$
$$x_{54} = -96.7458711524903$$
$$x_{55} = -76.0417247949483$$
$$x_{56} = 55.905166655823$$
$$x_{57} = 99.8874638060801$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{60} = 5.6396841983863$$
$$x_{61} = -88.6080954093075$$
$$x_{62} = 468.740806493672$$
$$x_{63} = 47.7673909126402$$
$$x_{64} = 62.1883519630026$$
$$x_{65} = 41.4842056054606$$
$$x_{66} = 49.6219813486434$$
$$x_{67} = -69.7585394877687$$
$$x_{68} = 43.3387960414638$$
$$x_{69} = -82.3249101021279$$
$$x_{70} = 3.78509376238308$$
$$x_{1} = -0.643501108793284$$
$$x_{2} = -19.493057030332$$
$$x_{3} = 66.6169468341789$$
$$x_{4} = 37.0556107342842$$
$$x_{5} = -15.0644621591557$$
$$x_{6} = -27.6308327735149$$
$$x_{7} = -107.457651330846$$
$$x_{8} = -94.8912807164871$$
$$x_{9} = 275.816652407109$$
$$x_{10} = 81.0379078845413$$
$$x_{11} = -13.2098717231525$$
$$x_{12} = 54.0505762198198$$
$$x_{13} = -63.4753541805892$$
$$x_{14} = 85.4665027557177$$
$$x_{15} = -40.197203387874$$
$$x_{16} = -46.4803886950536$$
$$x_{17} = -71.613129923772$$
$$x_{18} = -84.1795005381311$$
$$x_{19} = -33.9140180806944$$
$$x_{20} = -25.7762423375116$$
$$x_{21} = -50.90898356623$$
$$x_{22} = 91.7496880628973$$
$$x_{23} = 18.2060548127455$$
$$x_{24} = -101.174466023667$$
$$x_{25} = 16.3514643767422$$
$$x_{26} = 35.201020298281$$
$$x_{27} = 10.0682790695627$$
$$x_{28} = 87.3210931917209$$
$$x_{29} = 11.9228695055659$$
$$x_{30} = 139936.605069959$$
$$x_{31} = -8.7812768519761$$
$$x_{32} = -65.3299446165924$$
$$x_{33} = -77.8963152309515$$
$$x_{34} = -32.0594276446912$$
$$x_{35} = -59.0467593094128$$
$$x_{36} = -52.7635740022332$$
$$x_{37} = 93.6042784989005$$
$$x_{38} = 3280205.36115037$$
$$x_{39} = 60.3337615269994$$
$$x_{40} = -6.92668641597287$$
$$x_{41} = 79.1833174485381$$
$$x_{42} = -57.1921688734096$$
$$x_{43} = -2.49809154479651$$
$$x_{44} = 24.4892401199251$$
$$x_{45} = 30.7724254271046$$
$$x_{46} = 22.6346496839218$$
$$x_{47} = -38.3426129518708$$
$$x_{48} = 28.9178349911014$$
$$x_{49} = 68.4715372701822$$
$$x_{50} = -44.6257982590504$$
$$x_{51} = 98.0328733700769$$
$$x_{52} = -90.4626858453107$$
$$x_{53} = -21.3476474663353$$
$$x_{54} = -96.7458711524903$$
$$x_{55} = -76.0417247949483$$
$$x_{56} = 55.905166655823$$
$$x_{57} = 99.8874638060801$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{60} = 5.6396841983863$$
$$x_{61} = -88.6080954093075$$
$$x_{62} = 468.740806493672$$
$$x_{63} = 47.7673909126402$$
$$x_{64} = 62.1883519630026$$
$$x_{65} = 41.4842056054606$$
$$x_{66} = 49.6219813486434$$
$$x_{67} = -69.7585394877687$$
$$x_{68} = 43.3387960414638$$
$$x_{69} = -82.3249101021279$$
$$x_{70} = 3.78509376238308$$
This roots
$$x_{7} = -107.457651330846$$
$$x_{24} = -101.174466023667$$
$$x_{54} = -96.7458711524903$$
$$x_{8} = -94.8912807164871$$
$$x_{52} = -90.4626858453107$$
$$x_{61} = -88.6080954093075$$
$$x_{18} = -84.1795005381311$$
$$x_{69} = -82.3249101021279$$
$$x_{33} = -77.8963152309515$$
$$x_{55} = -76.0417247949483$$
$$x_{17} = -71.613129923772$$
$$x_{67} = -69.7585394877687$$
$$x_{32} = -65.3299446165924$$
$$x_{13} = -63.4753541805892$$
$$x_{35} = -59.0467593094128$$
$$x_{42} = -57.1921688734096$$
$$x_{36} = -52.7635740022332$$
$$x_{21} = -50.90898356623$$
$$x_{16} = -46.4803886950536$$
$$x_{50} = -44.6257982590504$$
$$x_{15} = -40.197203387874$$
$$x_{47} = -38.3426129518708$$
$$x_{19} = -33.9140180806944$$
$$x_{34} = -32.0594276446912$$
$$x_{6} = -27.6308327735149$$
$$x_{20} = -25.7762423375116$$
$$x_{53} = -21.3476474663353$$
$$x_{2} = -19.493057030332$$
$$x_{5} = -15.0644621591557$$
$$x_{11} = -13.2098717231525$$
$$x_{31} = -8.7812768519761$$
$$x_{40} = -6.92668641597287$$
$$x_{43} = -2.49809154479651$$
$$x_{1} = -0.643501108793284$$
$$x_{70} = 3.78509376238308$$
$$x_{60} = 5.6396841983863$$
$$x_{27} = 10.0682790695627$$
$$x_{29} = 11.9228695055659$$
$$x_{25} = 16.3514643767422$$
$$x_{23} = 18.2060548127455$$
$$x_{46} = 22.6346496839218$$
$$x_{44} = 24.4892401199251$$
$$x_{48} = 28.9178349911014$$
$$x_{45} = 30.7724254271046$$
$$x_{26} = 35.201020298281$$
$$x_{4} = 37.0556107342842$$
$$x_{65} = 41.4842056054606$$
$$x_{68} = 43.3387960414638$$
$$x_{63} = 47.7673909126402$$
$$x_{66} = 49.6219813486434$$
$$x_{12} = 54.0505762198198$$
$$x_{56} = 55.905166655823$$
$$x_{39} = 60.3337615269994$$
$$x_{64} = 62.1883519630026$$
$$x_{3} = 66.6169468341789$$
$$x_{49} = 68.4715372701822$$
$$x_{58} = 72.9001321413585$$
$$x_{59} = 74.7547225773617$$
$$x_{41} = 79.1833174485381$$
$$x_{10} = 81.0379078845413$$
$$x_{14} = 85.4665027557177$$
$$x_{28} = 87.3210931917209$$
$$x_{22} = 91.7496880628973$$
$$x_{37} = 93.6042784989005$$
$$x_{51} = 98.0328733700769$$
$$x_{57} = 99.8874638060801$$
$$x_{9} = 275.816652407109$$
$$x_{62} = 468.740806493672$$
$$x_{30} = 139936.605069959$$
$$x_{38} = 3280205.36115037$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{7}$$
For example, let's take the point
$$x_{0} = x_{7} - \frac{1}{10}$$
=
$$-107.457651330846 + - \frac{1}{10}$$
=
$$-107.557651330846$$
substitute to the expression
$$\sin{\left(t \right)} < - \frac{3}{5}$$
$$\sin{\left(t \right)} < - \frac{3}{5}$$
sin(t) < -3/5
Then
$$x < -107.457651330846$$
no execute
one of the solutions of our inequality is:
$$x > -107.457651330846 \wedge x < -101.174466023667$$
_____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____ _____
/ \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \
-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------ο-------
x7 x24 x54 x8 x52 x61 x18 x69 x33 x55 x17 x67 x32 x13 x35 x42 x36 x21 x16 x50 x15 x47 x19 x34 x6 x20 x53 x2 x5 x11 x31 x40 x43 x1 x70 x60 x27 x29 x25 x23 x46 x44 x48 x45 x26 x4 x65 x68 x63 x66 x12 x56 x39 x64 x3 x49 x58 x59 x41 x10 x14 x28 x22 x37 x51 x57 x9 x62 x30 x38Other solutions will get with the changeover to the next point
etc.
The answer:
$$x > -107.457651330846 \wedge x < -101.174466023667$$
$$x > -96.7458711524903 \wedge x < -94.8912807164871$$
$$x > -90.4626858453107 \wedge x < -88.6080954093075$$
$$x > -84.1795005381311 \wedge x < -82.3249101021279$$
$$x > -77.8963152309515 \wedge x < -76.0417247949483$$
$$x > -71.613129923772 \wedge x < -69.7585394877687$$
$$x > -65.3299446165924 \wedge x < -63.4753541805892$$
$$x > -59.0467593094128 \wedge x < -57.1921688734096$$
$$x > -52.7635740022332 \wedge x < -50.90898356623$$
$$x > -46.4803886950536 \wedge x < -44.6257982590504$$
$$x > -40.197203387874 \wedge x < -38.3426129518708$$
$$x > -33.9140180806944 \wedge x < -32.0594276446912$$
$$x > -27.6308327735149 \wedge x < -25.7762423375116$$
$$x > -21.3476474663353 \wedge x < -19.493057030332$$
$$x > -15.0644621591557 \wedge x < -13.2098717231525$$
$$x > -8.7812768519761 \wedge x < -6.92668641597287$$
$$x > -2.49809154479651 \wedge x < -0.643501108793284$$
$$x > 3.78509376238308 \wedge x < 5.6396841983863$$
$$x > 10.0682790695627 \wedge x < 11.9228695055659$$
$$x > 16.3514643767422 \wedge x < 18.2060548127455$$
$$x > 22.6346496839218 \wedge x < 24.4892401199251$$
$$x > 28.9178349911014 \wedge x < 30.7724254271046$$
$$x > 35.201020298281 \wedge x < 37.0556107342842$$
$$x > 41.4842056054606 \wedge x < 43.3387960414638$$
$$x > 47.7673909126402 \wedge x < 49.6219813486434$$
$$x > 54.0505762198198 \wedge x < 55.905166655823$$
$$x > 60.3337615269994 \wedge x < 62.1883519630026$$
$$x > 66.6169468341789 \wedge x < 68.4715372701822$$
$$x > 72.9001321413585 \wedge x < 74.7547225773617$$
$$x > 79.1833174485381 \wedge x < 81.0379078845413$$
$$x > 85.4665027557177 \wedge x < 87.3210931917209$$
$$x > 91.7496880628973 \wedge x < 93.6042784989005$$
$$x > 98.0328733700769 \wedge x < 99.8874638060801$$
$$x > 275.816652407109 \wedge x < 468.740806493672$$
$$x > 139936.605069959 \wedge x < 3280205.36115037$$
Rapid solution
[src]
And(t < -atan(3/4) + 2*pi, pi + atan(3/4) < t)
$$t < - \operatorname{atan}{\left(\frac{3}{4} \right)} + 2 \pi \wedge \operatorname{atan}{\left(\frac{3}{4} \right)} + \pi < t$$
(pi + atan(3/4) < t)∧(t < -atan(3/4) + 2*pi)
Rapid solution 2
[src]
(pi + atan(3/4), -atan(3/4) + 2*pi)
$$x\ in\ \left(\operatorname{atan}{\left(\frac{3}{4} \right)} + \pi, - \operatorname{atan}{\left(\frac{3}{4} \right)} + 2 \pi\right)$$
x in Interval.open(atan(3/4) + pi, -atan(3/4) + 2*pi)