sin(2x)cos(2x)<(1/4) inequation
The solution
You have entered
[src]
sin(2*x)*cos(2*x) < 1/4
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} < \frac{1}{4}$$
sin(2*x)*cos(2*x) < 1/4
Detail solution
Given the inequality:
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} < \frac{1}{4}$$
To solve this inequality, we must first solve the corresponding equation:
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} = \frac{1}{4}$$
Solve:
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
This roots
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{3}$$
For example, let's take the point
$$x_{0} = x_{3} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}$$
substitute to the expression
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} < \frac{1}{4}$$
$$\sin{\left(2 \left(- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}\right) \right)} \cos{\left(2 \left(- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}\right) \right)} < \frac{1}{4}$$
one of the solutions of our inequality is:
$$x < - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
Other solutions will get with the changeover to the next point
etc.
The answer:
$$x < - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x > - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)} \wedge x < - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x > \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} < \frac{1}{4}$$
To solve this inequality, we must first solve the corresponding equation:
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} = \frac{1}{4}$$
Solve:
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
This roots
$$x_{3} = - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x_{2} = - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)}$$
$$x_{4} = - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x_{1} = \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{3}$$
For example, let's take the point
$$x_{0} = x_{3} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}$$
=
$$- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}$$
substitute to the expression
$$\sin{\left(2 x \right)} \cos{\left(2 x \right)} < \frac{1}{4}$$
$$\sin{\left(2 \left(- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}\right) \right)} \cos{\left(2 \left(- \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)} - \frac{1}{10}\right) \right)} < \frac{1}{4}$$
/ / ___________\\ / / ___________\\
|1 | ___ / ___ || |1 | ___ / ___ ||
-cos|- + 2*atan\2 + \/ 3 + 2*\/ 2 + \/ 3 /|*sin|- + 2*atan\2 + \/ 3 + 2*\/ 2 + \/ 3 /| < 1/4
\5 / \5 /
one of the solutions of our inequality is:
$$x < - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
_____ _____ _____
\ / \ /
-------ο-------ο-------ο-------ο-------
x3 x2 x4 x1Other solutions will get with the changeover to the next point
etc.
The answer:
$$x < - \operatorname{atan}{\left(\sqrt{3} + 2 + 2 \sqrt{\sqrt{3} + 2} \right)}$$
$$x > - \operatorname{atan}{\left(- \sqrt{3} + 2 \sqrt{2 - \sqrt{3}} + 2 \right)} \wedge x < - \operatorname{atan}{\left(- 2 \sqrt{\sqrt{3} + 2} + \sqrt{3} + 2 \right)}$$
$$x > \operatorname{atan}{\left(-2 + 2 \sqrt{2 - \sqrt{3}} + \sqrt{3} \right)}$$
Solving inequality on a graph
Rapid solution 2
[src]
pi 5*pi pi
[0, --) U (----, --]
24 24 2
$$x\ in\ \left[0, \frac{\pi}{24}\right) \cup \left(\frac{5 \pi}{24}, \frac{\pi}{2}\right]$$
x in Union(Interval.Ropen(0, pi/24), Interval.Lopen(5*pi/24, pi/2))
Rapid solution
[src]
/ / pi\ / pi 5*pi \\ Or|And|0 <= x, x < --|, And|x <= --, ---- < x|| \ \ 24/ \ 2 24 //
$$\left(0 \leq x \wedge x < \frac{\pi}{24}\right) \vee \left(x \leq \frac{\pi}{2} \wedge \frac{5 \pi}{24} < x\right)$$
((0 <= x)∧(x < pi/24))∨((x <= pi/2)∧(5*pi/24 < x))

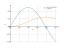 sin(2x)cos(2x)
sin(2x)cos(2x)