Mister Exam

Lang:

-4x^2+20x>25 inequation

You have entered [src]

     2            
- 4*x  + 20*x > 25

- 4 x^{2} + 20 x > 25

-4*x^2 + 20*x > 25

Detail solution

Given the inequality:

- 4 x^{2} + 20 x > 25

To solve this inequality, we must first solve the corresponding equation:

- 4 x^{2} + 20 x = 25

Solve:
Move right part of the equation to
left part with negative sign.

The equation is transformed from

- 4 x^{2} + 20 x = 25

\left(- 4 x^{2} + 20 x\right) - 25 = 0

This equation is of the form

a*x^2 + b*x + c = 0

A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:

x_{1} = \frac{\sqrt{D} - b}{2 a}

x_{2} = \frac{- \sqrt{D} - b}{2 a}

where D = b^2 - 4*a*c - it is the discriminant.
Because

a = -4

b = 20

c = -25

, then

D = b^2 - 4 * a * c =

(20)^2 - 4 * (-4) * (-25) = 0

Because D = 0, then the equation has one root.

x = -b/2a = -20/2/(-4)

x_{1} = \frac{5}{2}

x_{1} = \frac{5}{2}

x_{1} = \frac{5}{2}

This roots

x_{1} = \frac{5}{2}

is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:

x_{0} < x_{1}

For example, let's take the point

x_{0} = x_{1} - \frac{1}{10}

- \frac{1}{10} + \frac{5}{2}

\frac{12}{5}

substitute to the expression

- 4 x^{2} + 20 x > 25

- 4 \left(\frac{12}{5}\right)^{2} + \frac{12 \cdot 20}{5} > 25

624     
--- > 25
 25

Then

x < \frac{5}{2}

no execute
the solution of our inequality is:

x > \frac{5}{2}

         _____  
        /
-------ο-------
       x1

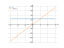
Solving inequality on a graph

Rapid solution

This inequality has no solutions