Derivative of 3xlogx
The solution
Detail solution
-
Apply the product rule:
; to find :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
; to find :
-
The derivative of is .
The result is:
-
The answer is:
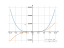
The graph


![Find the derivative of y' = f'(x) = 3xlogx (3x logarithm of x) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] 3xlogx](/media/krcore-image-pods/176/c/87/5744b1df463d6e2c3cc7d6cbe8c74.png)
 Derivative of 7x^5
Derivative of 7x^5
 Derivative of 3xlogx
Derivative of 3xlogx
 Derivative of 3x^4-2
Derivative of 3x^4-2