Mister Exam
Other calculators:
-
How to use it?
- Limit of the function:
-
Limit of (1+3*x)^(5/x)
-
Limit of x^2/(-2+sqrt(4+x^2))
-
Limit of ((5+x^2-6*x)/(5+x^2-5*x))^(2+3*x)
-
Limit of (2+x^2+3*x)/(-4+x^2)
- Derivative of:
-
x^(1/x)
- Graphing y =:
- x^(1/x)
- Integral of d{x}:
- x^(1/x)
-
Identical expressions
- x^(one /x)
- x to the power of (1 divide by x)
- x to the power of (one divide by x)
- x(1/x)
- x1/x
- x^1/x
- x^(1 divide by x)
-
Similar expressions
- (x+e^(3*x))^(1/x)
- factorial(x)^(1/x)
- sin(1/x)^(1/x)
- x*factorial(x)^(1/x)
- (1-5*x)^(1/x)
Limit of the function x^(1/x)
The solution
You have entered
[src]
x ___ lim \/ x x->oo
$$\lim_{x \to \infty} x^{\frac{1}{x}}$$
Limit(x^(1/x), x, oo, dir='-')
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
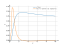
The graph
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to \infty} x^{\frac{1}{x}} = 1$$
$$\lim_{x \to 0^-} x^{\frac{1}{x}} = \infty$$
More at x→0 from the left
$$\lim_{x \to 0^+} x^{\frac{1}{x}} = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-} x^{\frac{1}{x}} = 1$$
More at x→1 from the left
$$\lim_{x \to 1^+} x^{\frac{1}{x}} = 1$$
More at x→1 from the right
$$\lim_{x \to -\infty} x^{\frac{1}{x}} = 1$$
More at x→-oo
$$\lim_{x \to 0^-} x^{\frac{1}{x}} = \infty$$
More at x→0 from the left
$$\lim_{x \to 0^+} x^{\frac{1}{x}} = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-} x^{\frac{1}{x}} = 1$$
More at x→1 from the left
$$\lim_{x \to 1^+} x^{\frac{1}{x}} = 1$$
More at x→1 from the right
$$\lim_{x \to -\infty} x^{\frac{1}{x}} = 1$$
More at x→-oo
The graph