Integrale doppio passo dopo passo

Con la soluzione corretta dell'integrale sarai il più amato del gruppo ❤️😊

Seleziona il tipo di integrale doppio ∫∫dxdy

∫

∫∫
D

d d

Specifica l'area D:

Cosa sa fare?

Calcola l'integrale doppio sull'area delimitata dalle linee indicate (qui), determinando così i limiti di integrazione in esso qui
Calcola tramite integrale doppio l'area della figura delimitata da linee
Calcola integrali iterati (con limiti già noti)
Scrive l'integrale doppio di f(x, y) come integrale iterato
Calcola la massa di una lamina tramite integrale doppio
Scambio dell'ordine di integrazione nell'integrale iterato (qui)
Se ha senso usare polari coordinate, allora vengono usate

Calcolo dell'area

Per calcolare l'area della figura delimitata da linee mediante integrale doppio, sostituisci 1 nella funzione integranda. Puoi anche usare la seguente calcolatrice: Area tra le curve

Esempi di integrali doppi

Con il quadrato
```
8*x*y+9*x^2*y^2
```
Con il cubo
```
x^3+x*y^2
```
Con seno e radice quadrata
```
sin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2)
```
Funzione lineare
```
2*x + y
```
Trovare l'area della figura delimitata da curve tramite integrale doppio
```
x^3*y^2
```
Cambiare l'ordine di integrazione nell'integrale doppio
```
x^3*y^2
```
Integrale doppio sulla regione delimitata da linee curve
```
x^3*y^2
```
Impostare i limiti di integrazione nell’integrale doppio
```
x^3*y^2
```
Integrale doppio nel sistema polare
```
e^(x^2+y^2)
```
```
yln(1-x^2-y^2)/(x-sqrt(x^2+y^2))
```

Come specificare l'area D?

L'area D può essere specificata in modi diversi:

Con linee curve:
1. Circonferenza
2. Due cerchi
3. Ellisse
4. Parabola
5. Altri
Con i vertici:
1. Triangolo
```
A(0, 1)
```
```
B(1, 0)
```
```
C(0, 0)
```
2. Quadrato
3. Rettangolo
e — quadrante

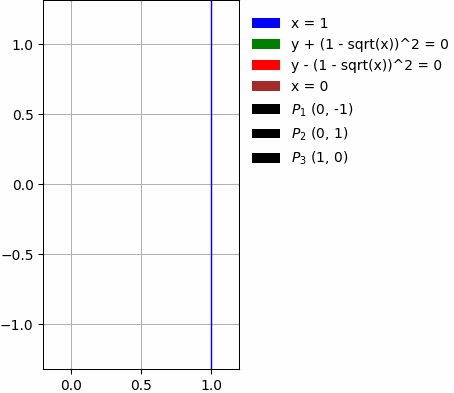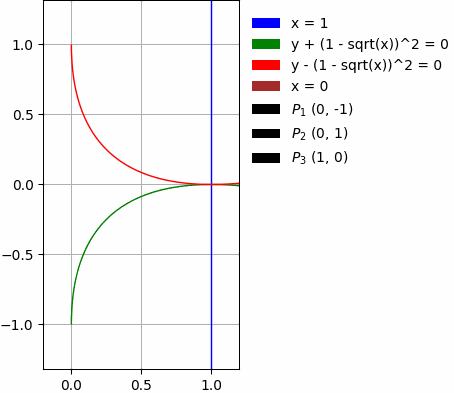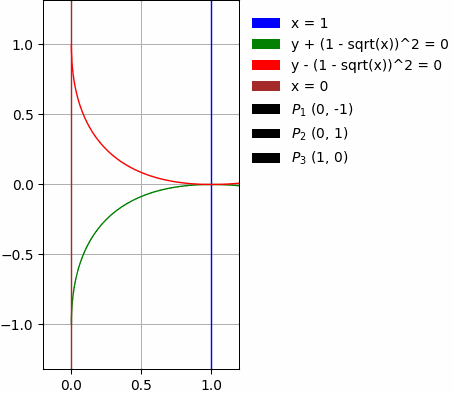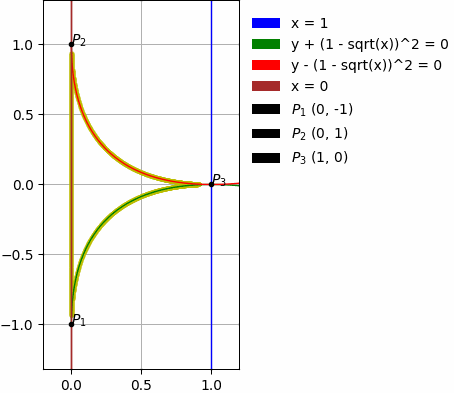
Come disuguaglianza

Imposta il vincolo per l'area di integrazione sotto forma di disuguaglianza:

x > pi/2

-1/2 < y <= 3/2

x < sqrt(2)/2 + 1

Gli esempi sopra indicati contengono anche:

modulo oppure valore assoluto: absolute(x) oppure |x|
radici quadrate sqrt(x),
radici cubiche cbrt(x)
funzioni trigonometriche:
seno sin(x), coseno cos(x), tangente tan(x), cotangente ctan(x)
funzioni esponenziali e l'esponenziale exp(x)
funzioni trigonometriche inverse:
arcseno asin(x), arcocoseno acos(x), arcotangente atan(x), arcocotangente acot(x)
logaritmi naturali ln(x),
logaritmi decimali log(x)
funzioni iperboliche:
seno iperbolico sh(x), coseno iperbolico ch(x), tangente e cotangente iperboliche tanh(x), ctanh(x)
funzioni iperboliche inverse:
arcseno iperbolico asinh(x), arcocoseno iperbolico acosh(x), arcotangente iperbolica atanh(x), arcocotangente iperbolica acoth(x)
altre funzioni trigonometriche e iperboliche:
secante sec(x), cosecante csc(x), arcsecante asec(x), arccosecante acsc(x), secante iperbolica sech(x), cosecante iperbolica csch(x), arcsecante iperbolica asech(x), arccosecante iperbolica acsch(x)
funzioni di arrotondamento:
per difetto floor(x), per eccesso ceiling(x)
segno del numero:
sign(x)
per la teoria della probabilità:
funzione di errore erf(x) (integrale di probabilità), funzione di Laplace laplace(x)
Fattoriale di x:
x! oppure factorial(x)
funzione Gamma gamma(x)
funzione di Lambert LambertW(x)
integrali trigonometrici: Si(x), Ci(x), Shi(x), Chi(x)

Regole di input

Si possono fare le seguenti operazioni

2*x: - moltiplicazione
3/x: - divisione
x^2: - elevamento al quadrato
x^3: - elevamento al cubo
x^5: - elevamento a potenza
x + 7: - addizione
x - 6: - sottrazione
Numeri reali: inserire nella forma 7.5, non 7,5

Costanti

pi: - pi greco
e: - base del logaritmo naturale
i: - numero complesso
oo: - simbolo dell'infinito

Questi esempi possono essere utilizzati anche quando si inseriscono i limiti superiori e inferiori nell'integrale doppio.

Altri calcolatori