Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of x/(1+x)
-
Integral of x/e^x
-
Integral of e^(-3x)
-
Integral of 11
-
Identical expressions
- (3x- two)/(x^ two + nine)
- (3x minus 2) divide by (x squared plus 9)
- (3x minus two) divide by (x to the power of two plus nine)
- (3x-2)/(x2+9)
- 3x-2/x2+9
- (3x-2)/(x²+9)
- (3x-2)/(x to the power of 2+9)
- 3x-2/x^2+9
- (3x-2) divide by (x^2+9)
- (3x-2)/(x^2+9)dx
-
Similar expressions
- (3x-2)/(x^2-9)
- (3x+2)/(x^2+9)
Integral of (3x-2)/(x^2+9) dx
The solution
You have entered
[src]
1 / | | 3*x - 2 | ------- dx | 2 | x + 9 | / 0
$$\int\limits_{0}^{1} \frac{3 x - 2}{x^{2} + 9}\, dx$$
Integral((3*x - 1*2)/(x^2 + 9), (x, 0, 1))
Detail solution
We have the integral:
/ | | 3*x - 2 | 1*------- dx | 2 | x + 9 | /
Rewrite the integrand
1*2*x + 0
3*-------------- /-2 \
2 |---|
3*x - 2 1*x + 0*x + 9 \ 9 /
------- = ---------------- + --------------
2 2 2
x + 9 / x \
|- - + 0| + 1
\ 3 / or
/ | | 3*x - 2 | 1*------- dx | 2 = | x + 9 | /
/
|
| 1 /
2* | -------------- dx |
| 2 | 1*2*x + 0
| / x \ 3* | -------------- dx
| |- - + 0| + 1 | 2
| \ 3 / | 1*x + 0*x + 9
| |
/ /
- ---------------------- + ----------------------
9 2 In the integral
/
|
| 1*2*x + 0
3* | -------------- dx
| 2
| 1*x + 0*x + 9
|
/
----------------------
2 do replacement
2 u = x
then
the integral =
/
|
| 1
3* | ----- du
| 9 + u
|
/ 3*log(9 + u)
------------- = ------------
2 2 do backward replacement
/
|
| 1*2*x + 0
3* | -------------- dx
| 2
| 1*x + 0*x + 9
| / 2\
/ 3*log\9 + x /
---------------------- = -------------
2 2 In the integral
/
|
| 1
-2* | -------------- dx
| 2
| / x \
| |- - + 0| + 1
| \ 3 /
|
/
-----------------------
9 do replacement
-x
v = ---
3 then
the integral =
/
|
| 1
-2* | ------ dv
| 2
| 1 + v
|
/ -2*atan(v)
--------------- = ----------
9 9 do backward replacement
/
|
| 1
-2* | -------------- dx
| 2
| / x \
| |- - + 0| + 1
| \ 3 / /x\
| -2*atan|-|
/ \3/
----------------------- = ----------
9 3 Solution is:
/x\
2*atan|-| / 2\
\3/ 3*log\9 + x /
C - --------- + -------------
3 2
The answer (Indefinite)
[src]
/ /x\ | 2*atan|-| / 2\ | 3*x - 2 \3/ 3*log\9 + x / | ------- dx = C - --------- + ------------- | 2 3 2 | x + 9 | /
$${{3\,\log \left(x^2+9\right)}\over{2}}-{{2\,\arctan \left({{x
}\over{3}}\right)}\over{3}}$$
The graph
The answer
[src]
3*log(9) 2*atan(1/3) 3*log(10)
- -------- - ----------- + ---------
2 3 2
$${{3\,\log 10}\over{2}}-{{3\,\log 9}\over{2}}-{{2\,\arctan \left({{1
}\over{3}}\right)}\over{3}}$$
=
=
3*log(9) 2*atan(1/3) 3*log(10)
- -------- - ----------- + ---------
2 3 2
$$- \frac{3 \log{\left(9 \right)}}{2} - \frac{2 \operatorname{atan}{\left(\frac{1}{3} \right)}}{3} + \frac{3 \log{\left(10 \right)}}{2}$$
The graph
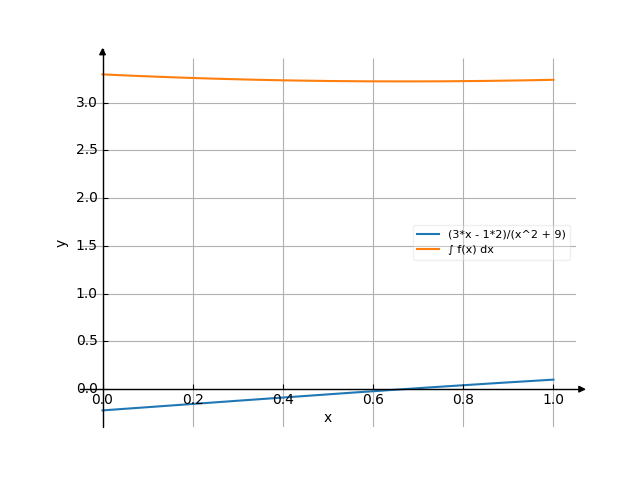
Use the examples entering the upper and lower limits of integration.