sin(3*x)>-sqrt(3)/2 inequation
The solution
Detail solution
Given the inequality:
To solve this inequality, we must first solve the corresponding equation:
Solve:
Given the equation
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
Divide both parts of the equation by
This roots
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
For example, let's take the point
=
=
substitute to the expression
Then
no execute
one of the solutions of our inequality is:
To solve this inequality, we must first solve the corresponding equation:
Solve:
Given the equation
- this is the simplest trigonometric equation
This equation is transformed to
Or
, where n - is a integer
Divide both parts of the equation by
This roots
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
For example, let's take the point
=
=
substitute to the expression
___
/3 pi \ -\/ 3
-sin|-- + -- - 2*pi*n| > -------
\10 3 / 2
Then
no execute
one of the solutions of our inequality is:
_____
/ \
-------ο-------ο-------
x1 x2
Solving inequality on a graph
Rapid solution
[src]
/ / 4*pi\ / 2*pi 5*pi \\ Or|And|0 <= x, x < ----|, And|x <= ----, ---- < x|| \ \ 9 / \ 3 9 //
((0 <= x)∧(x < 4*pi/9))∨((x <= 2*pi/3)∧(5*pi/9 < x))
Rapid solution 2
[src]
4*pi 5*pi 2*pi
[0, ----) U (----, ----]
9 9 3
x in Union(Interval.Ropen(0, 4*pi/9), Interval.Lopen(5*pi/9, 2*pi/3))

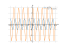 sin(3*x)
sin(3*x)
 sin(3*x)
sin(3*x)