Area between lines

The teacher will be very surprised to see your correct solution 😉

What can it do?

• Detect intersection points of the curves
• Smart robot detect the contours and its regions and general regions, where we define curves, then the one calculate there areas. The robot do this via line intersection points
• Helps to find the area under (or between) plot curves via calculating integrals
• Support for Cartesian, parametric, and polar coordinates

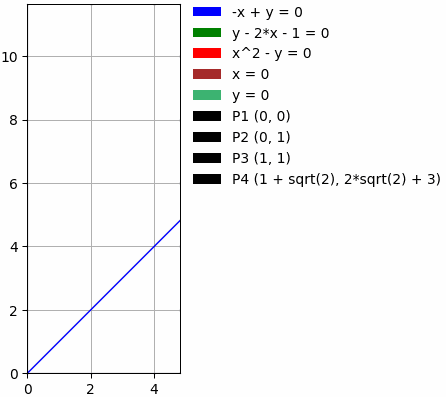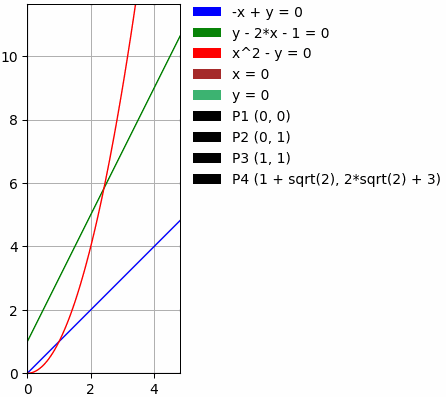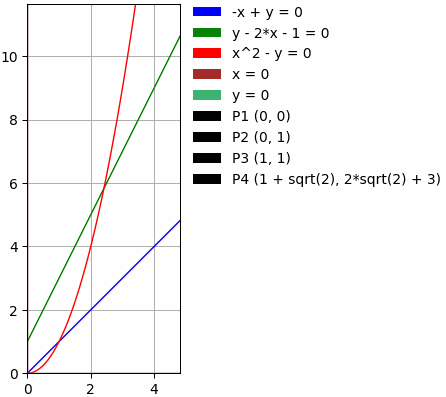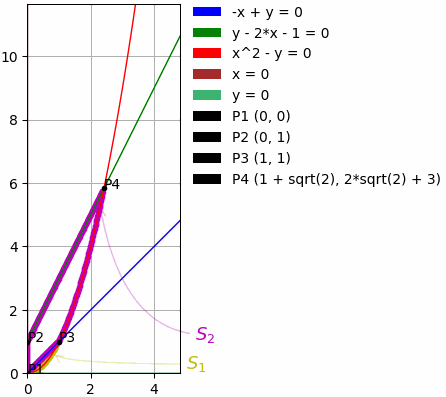
Examples of curves

The above examples also contain:

• the modulus or absolute value: absolute(x) or |x|
• square roots sqrt(x),
  cubic roots cbrt(x)
• trigonometric functions:
  sinus sin(x), cosine cos(x), tangent tan(x), cotangent ctan(x)
• exponential functions and exponents exp(x)
• inverse trigonometric functions:
  arcsine asin(x), arccosine acos(x), arctangent atan(x), arccotangent acot(x)
• natural logarithms ln(x),
  decimal logarithms log(x)
• hyperbolic functions:
  hyperbolic sine sh(x), hyperbolic cosine ch(x), hyperbolic tangent and cotangent tanh(x), ctanh(x)
• inverse hyperbolic functions:
  hyperbolic arcsine asinh(x), hyperbolic arccosinus acosh(x), hyperbolic arctangent atanh(x), hyperbolic arccotangent acoth(x)
• other trigonometry and hyperbolic functions:
  secant sec(x), cosecant csc(x), arcsecant asec(x), arccosecant acsc(x), hyperbolic secant sech(x), hyperbolic cosecant csch(x), hyperbolic arcsecant asech(x), hyperbolic arccosecant acsch(x)
• rounding functions:
  round down floor(x), round up ceiling(x)
• the sign of a number:
  sign(x)
• for probability theory:
  the error function erf(x) (integral of probability), Laplace function laplace(x)
• Factorial of x:
  x! or factorial(x)
• Gamma function gamma(x)
• Lambert's function LambertW(x)
• Trigonometric integrals: Si(x), Ci(x), Shi(x), Chi(x)

The insertion rules

The following operations can be performed

2*x

- multiplication

3/x

- division

x^2

- squaring

x^3

- cubing

x^5

- raising to the power

x + 7

- addition

x - 6

- subtraction

Real numbers

insert as 7.5, no 7,5

Constants

pi

- number Pi

e

- the base of natural logarithm

i

- complex number

oo

- symbol of infinity

Include inequalities in the region

In addition to curves, the region can be further bounded by specifying inequalities:

x > pi/2

-1/2 < y <= 3/2

x < sqrt(2)/2 + 1

You can also find the area of the shape via double integral