Mister Exam

Other calculators

Plotting a function graph/ sqrt(x^2)

Graphing y = sqrt(x^2)

v

The graph:

from to

Intersection points:

does show?

Piecewise:

The solution

You have entered [src] 
          ____
         /  2 
f(x) = \/  x
f(x)=x2f{\left(x \right)} = \sqrt{x^{2}} 
f = sqrt(x^2)
The graph of the function
0.01.02.03.04.05.06.07.08.09.010.0020
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
x2=0\sqrt{x^{2}} = 0
Solve this equation
The points of intersection with the axis X:

Analytical solution
x1=0x_{1} = 0
Numerical solution
x1=0x_{1} = 0
The points of intersection with the Y axis coordinate
The graph crosses Y axis when x equals 0:
substitute x = 0 to sqrt(x^2).
02\sqrt{0^{2}}
The result:
f(0)=0f{\left(0 \right)} = 0
The point:
(0, 0)
Extrema of the function
In order to find the extrema, we need to solve the equation
ddxf(x)=0\frac{d}{d x} f{\left(x \right)} = 0
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
ddxf(x)=\frac{d}{d x} f{\left(x \right)} =
the first derivative
∣x∣x=0\frac{\left|{x}\right|}{x} = 0
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
d2dx2f(x)=0\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
d2dx2f(x)=\frac{d^{2}}{d x^{2}} f{\left(x \right)} =
the second derivative
sign⁡(x)−∣x∣xx=0\frac{\operatorname{sign}{\left(x \right)} - \frac{\left|{x}\right|}{x}}{x} = 0
Solve this equation
The roots of this equation
x1=66x_{1} = 66
x2=94x_{2} = 94
x3=98x_{3} = 98
x4=46x_{4} = 46
x5=24x_{5} = 24
x6=−24x_{6} = -24
x7=−46x_{7} = -46
x8=18x_{8} = 18
x9=22x_{9} = 22
x10=−82x_{10} = -82
x11=−74x_{11} = -74
x12=−42x_{12} = -42
x13=50x_{13} = 50
x14=64x_{14} = 64
x15=36x_{15} = 36
x16=−60x_{16} = -60
x17=−66x_{17} = -66
x18=−8x_{18} = -8
x19=−26x_{19} = -26
x20=−2x_{20} = -2
x21=86x_{21} = 86
x22=42x_{22} = 42
x23=−36x_{23} = -36
x24=100x_{24} = 100
x25=−18x_{25} = -18
x26=12x_{26} = 12
x27=90x_{27} = 90
x28=−88x_{28} = -88
x29=−92x_{29} = -92
x30=52x_{30} = 52
x31=−44x_{31} = -44
x32=6x_{32} = 6
x33=38x_{33} = 38
x34=96x_{34} = 96
x35=−84x_{35} = -84
x36=10x_{36} = 10
x37=−98x_{37} = -98
x38=62x_{38} = 62
x39=−28x_{39} = -28
x40=14x_{40} = 14
x41=30x_{41} = 30
x42=−14x_{42} = -14
x43=−72x_{43} = -72
x44=−20x_{44} = -20
x45=54x_{45} = 54
x46=−52x_{46} = -52
x47=−12x_{47} = -12
x48=68x_{48} = 68
x49=32x_{49} = 32
x50=28x_{50} = 28
x51=−16x_{51} = -16
x52=−40x_{52} = -40
x53=−48x_{53} = -48
x54=44x_{54} = 44
x55=−6x_{55} = -6
x56=−50x_{56} = -50
x57=16x_{57} = 16
x58=−78x_{58} = -78
x59=4x_{59} = 4
x60=−56x_{60} = -56
x61=−10x_{61} = -10
x62=74x_{62} = 74
x63=−34x_{63} = -34
x64=−62x_{64} = -62
x65=−58x_{65} = -58
x66=84x_{66} = 84
x67=−68x_{67} = -68
x68=76x_{68} = 76
x69=−94x_{69} = -94
x70=−86x_{70} = -86
x71=−4x_{71} = -4
x72=40x_{72} = 40
x73=−96x_{73} = -96
x74=−70x_{74} = -70
x75=8x_{75} = 8
x76=82x_{76} = 82
x77=−80x_{77} = -80
x78=−76x_{78} = -76
x79=−38x_{79} = -38
x80=−32x_{80} = -32
x81=−30x_{81} = -30
x82=−54x_{82} = -54
x83=48x_{83} = 48
x84=20x_{84} = 20
x85=56x_{85} = 56
x86=58x_{86} = 58
x87=78x_{87} = 78
x88=70x_{88} = 70
x89=60x_{89} = 60
x90=92x_{90} = 92
x91=−90x_{91} = -90
x92=72x_{92} = 72
x93=88x_{93} = 88
x94=2x_{94} = 2
x95=−64x_{95} = -64
x96=−100x_{96} = -100
x97=80x_{97} = 80
x98=−22x_{98} = -22
x99=34x_{99} = 34
x100=26x_{100} = 26

Сonvexity and concavity intervals:
Let’s find the intervals where the function is convex or concave, for this look at the behaviour of the function at the inflection points:
Concave at the intervals
[−30,30]\left[-30, 30\right]
Convex at the intervals
(−∞,−30]∪[30,∞)\left(-\infty, -30\right] \cup \left[30, \infty\right)
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
lim⁡x→−∞x2=∞\lim_{x \to -\infty} \sqrt{x^{2}} = \infty
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
lim⁡x→∞x2=∞\lim_{x \to \infty} \sqrt{x^{2}} = \infty
Let's take the limit
so,
horizontal asymptote on the right doesn’t exist
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of sqrt(x^2), divided by x at x->+oo and x ->-oo
lim⁡x→−∞(∣x∣x)=−1\lim_{x \to -\infty}\left(\frac{\left|{x}\right|}{x}\right) = -1
Let's take the limit
so,
inclined asymptote equation on the left:
y=−xy = - x
lim⁡x→∞(∣x∣x)=1\lim_{x \to \infty}\left(\frac{\left|{x}\right|}{x}\right) = 1
Let's take the limit
so,
inclined asymptote equation on the right:
y=xy = x
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
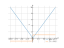x2=x2\sqrt{x^{2}} = \sqrt{x^{2}}
- Yes
x2=−x2\sqrt{x^{2}} = - \sqrt{x^{2}}
- No
so, the function
is
even
    © Mister Exam – Calculator