Mister Exam
Other calculators
- Graph of implicit function
- Derivative Step by Step
- Integral Step by Step
- Graph of parametric function
- Graph in Polar Coordinates
- Surface defined parametrically
- Surface defined by equation
- Curve in 3D space defined parametrically
- Area between lines
- The intersection points of functions
-
How to use it?
- Graphing y =:
- x^3+4x-7
- (4x^2+1)/x
- x+cosx
- -x^4+4x^3+1
- Integral of d{x}:
-
sqrt(x^2+1)/x
- Derivative of:
-
sqrt(x^2+1)/x
-
Identical expressions
- sqrt(x^ two + one)/x
- square root of (x squared plus 1) divide by x
- square root of (x to the power of two plus one) divide by x
- √(x^2+1)/x
- sqrt(x2+1)/x
- sqrtx2+1/x
- sqrt(x²+1)/x
- sqrt(x to the power of 2+1)/x
- sqrtx^2+1/x
- sqrt(x^2+1) divide by x
-
Similar expressions
- sqrt(x^2-1)/x
-
What you mean?
- sqrt(x^2 + 1)/x
- sqrt(x*(2 + 1))/x
- sqrt(x^(2 + 1))/x
- sqrt(x^2 + 1)/x
- sqrt(x^2 + 1)/x
You entered:
sqrt(x^2+1)/x
What you mean?
Graphing y = sqrt(x^2+1)/x
The solution
You have entered
[src]
________
/ 2
\/ x + 1
f(x) = -----------
x
$$f{\left(x \right)} = \frac{\sqrt{x^{2} + 1}}{x}$$
f = sqrt(x^2 + 1)/x
The graph of the function
The domain of the function
The points at which the function is not precisely defined:
$$x_{1} = 0$$
$$x_{1} = 0$$
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
$$\frac{\sqrt{x^{2} + 1}}{x} = 0$$
Solve this equation
Solution is not found,
it's possible that the graph doesn't intersect the axis X
so we need to solve the equation:
$$\frac{\sqrt{x^{2} + 1}}{x} = 0$$
Solve this equation
Solution is not found,
it's possible that the graph doesn't intersect the axis X
Extrema of the function
In order to find the extrema, we need to solve the equation
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{1}{\sqrt{x^{2} + 1}} - \frac{\sqrt{x^{2} + 1}}{x^{2}} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
$$\frac{d}{d x} f{\left(x \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d x} f{\left(x \right)} = $$
the first derivative
$$\frac{1}{\sqrt{x^{2} + 1}} - \frac{\sqrt{x^{2} + 1}}{x^{2}} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$\frac{- \frac{\frac{x^{2}}{x^{2} + 1} - 1}{\sqrt{x^{2} + 1}} - \frac{2}{\sqrt{x^{2} + 1}} + \frac{2 \sqrt{x^{2} + 1}}{x^{2}}}{x} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d x^{2}} f{\left(x \right)} = $$
the second derivative
$$\frac{- \frac{\frac{x^{2}}{x^{2} + 1} - 1}{\sqrt{x^{2} + 1}} - \frac{2}{\sqrt{x^{2} + 1}} + \frac{2 \sqrt{x^{2} + 1}}{x^{2}}}{x} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
Vertical asymptotes
Have:
$$x_{1} = 0$$
$$x_{1} = 0$$
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
$$\lim_{x \to -\infty}\left(\frac{\sqrt{x^{2} + 1}}{x}\right) = -1$$
Let's take the limit
so,
equation of the horizontal asymptote on the left:
$$y = -1$$
$$\lim_{x \to \infty}\left(\frac{\sqrt{x^{2} + 1}}{x}\right) = 1$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = 1$$
$$\lim_{x \to -\infty}\left(\frac{\sqrt{x^{2} + 1}}{x}\right) = -1$$
Let's take the limit
so,
equation of the horizontal asymptote on the left:
$$y = -1$$
$$\lim_{x \to \infty}\left(\frac{\sqrt{x^{2} + 1}}{x}\right) = 1$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = 1$$
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of sqrt(x^2 + 1)/x, divided by x at x->+oo and x ->-oo
$$\lim_{x \to -\infty}\left(\frac{\sqrt{x^{2} + 1}}{x^{2}}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the right
$$\lim_{x \to \infty}\left(\frac{\sqrt{x^{2} + 1}}{x^{2}}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
$$\lim_{x \to -\infty}\left(\frac{\sqrt{x^{2} + 1}}{x^{2}}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the right
$$\lim_{x \to \infty}\left(\frac{\sqrt{x^{2} + 1}}{x^{2}}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
$$\frac{\sqrt{x^{2} + 1}}{x} = - \frac{\sqrt{x^{2} + 1}}{x}$$
- No
$$\frac{\sqrt{x^{2} + 1}}{x} = \frac{\sqrt{x^{2} + 1}}{x}$$
- No
so, the function
not is
neither even, nor odd
So, check:
$$\frac{\sqrt{x^{2} + 1}}{x} = - \frac{\sqrt{x^{2} + 1}}{x}$$
- No
$$\frac{\sqrt{x^{2} + 1}}{x} = \frac{\sqrt{x^{2} + 1}}{x}$$
- No
so, the function
not is
neither even, nor odd
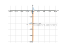
The graph