Graphing y = e^(-n)
The solution
The graph of the function
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis N at f = 0
so we need to solve the equation:
$$e^{- n} = 0$$
Solve this equation
Solution is not found,
it's possible that the graph doesn't intersect the axis N
so we need to solve the equation:
$$e^{- n} = 0$$
Solve this equation
Solution is not found,
it's possible that the graph doesn't intersect the axis N
Extrema of the function
In order to find the extrema, we need to solve the equation
$$\frac{d}{d n} f{\left(n \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d n} f{\left(n \right)} = $$
the first derivative
$$- e^{- n} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
$$\frac{d}{d n} f{\left(n \right)} = 0$$
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
$$\frac{d}{d n} f{\left(n \right)} = $$
the first derivative
$$- e^{- n} = 0$$
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
$$\frac{d^{2}}{d n^{2}} f{\left(n \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d n^{2}} f{\left(n \right)} = $$
the second derivative
$$e^{- n} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
$$\frac{d^{2}}{d n^{2}} f{\left(n \right)} = 0$$
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
$$\frac{d^{2}}{d n^{2}} f{\left(n \right)} = $$
the second derivative
$$e^{- n} = 0$$
Solve this equation
Solutions are not found,
maybe, the function has no inflections
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at n->+oo and n->-oo
$$\lim_{n \to -\infty} e^{- n} = \infty$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{n \to \infty} e^{- n} = 0$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = 0$$
$$\lim_{n \to -\infty} e^{- n} = \infty$$
Let's take the limit
so,
horizontal asymptote on the left doesn’t exist
$$\lim_{n \to \infty} e^{- n} = 0$$
Let's take the limit
so,
equation of the horizontal asymptote on the right:
$$y = 0$$
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of E^(-n), divided by n at n->+oo and n ->-oo
$$\lim_{n \to -\infty}\left(\frac{e^{- n}}{n}\right) = -\infty$$
Let's take the limit
so,
inclined asymptote on the left doesn’t exist
$$\lim_{n \to \infty}\left(\frac{e^{- n}}{n}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
$$\lim_{n \to -\infty}\left(\frac{e^{- n}}{n}\right) = -\infty$$
Let's take the limit
so,
inclined asymptote on the left doesn’t exist
$$\lim_{n \to \infty}\left(\frac{e^{- n}}{n}\right) = 0$$
Let's take the limit
so,
inclined coincides with the horizontal asymptote on the left
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-n) и f = -f(-n).
So, check:
$$e^{- n} = e^{n}$$
- No
$$e^{- n} = - e^{n}$$
- No
so, the function
not is
neither even, nor odd
So, check:
$$e^{- n} = e^{n}$$
- No
$$e^{- n} = - e^{n}$$
- No
so, the function
not is
neither even, nor odd

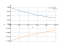 e^(-n)
e^(-n)
 e^(-n)
e^(-n)
 e^(-n)
e^(-n)