Mister Exam

Lang:

Outras calculadoras

Como usar?
Derivada:
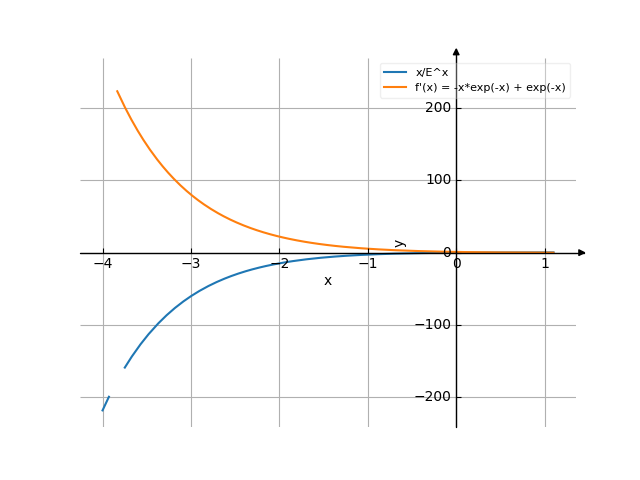
Derivada x*e^(-x)
Derivada f(x)=5x-9
Derivada f(x)=5x³-4x²-3x+2
Derivada f(x)
Gráfico da função y =:
x*e^(-x)
Integral d{x}:
x*e^(-x)
Limite da função:
x*e^(-x)
Expressões idênticas
x*e^(-x)
x multiplicar por e elevado a ( menos x)
x*e(-x)
x*e-x
xe^(-x)
xe(-x)
xe-x
xe^-x
Expressões semelhantes
sin(x)*e^(-x)
-2xe^(-x^2)
x*e^(x)
5*tan(x)^3+sin(4*x)*e^((-x)/7)

Derivada de função/ x*e^(-x)

Derivada x*e^(-x)

Find the 200th derivative of f(x) = xe−x.
Find the 600th derivative of f(x) = xe−x.

A solução

You have entered [src]

   -x
x*e

$$x e^{- x}$$

d /   -x\
--\x*e  /
dx

$$\frac{d}{d x} x e^{- x}$$

Transform

Detail solution

Apply the quotient rule, which is:

$\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$

$f{\left(x \right)} = x$ and $g{\left(x \right)} = e^{x}$ .

To find $\frac{d}{d x} f{\left(x \right)}$ :
1. Apply the power rule: $x$ goes to $1$
To find $\frac{d}{d x} g{\left(x \right)}$ :
1. The derivative of $e^{x}$ is itself.
Now plug in to the quotient rule:

$\left(- x e^{x} + e^{x}\right) e^{- 2 x}$
Now simplify:

$\left(1 - x\right) e^{- x}$

The answer is:

$\left(1 - x\right) e^{- x}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

 -x      -x
e   - x*e

$$- x e^{- x} + e^{- x}$$

Simplify

The second derivative [src]

          -x
(-2 + x)*e

$$\left(x - 2\right) e^{- x}$$

Simplify

The third derivative [src]

         -x
(3 - x)*e

$$\left(3 - x\right) e^{- x}$$

Simplify

Gráfico

Derivada x*e^(-x)