Adım adım seri toplamı
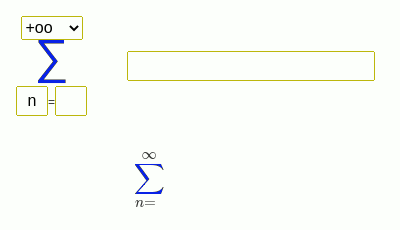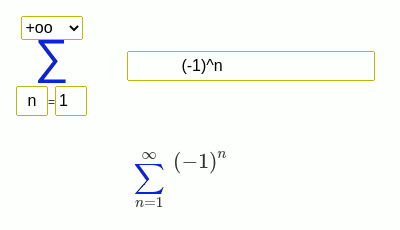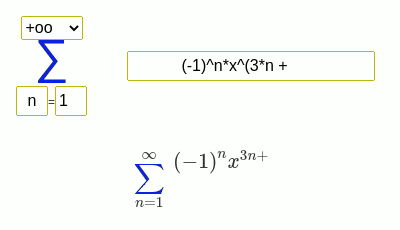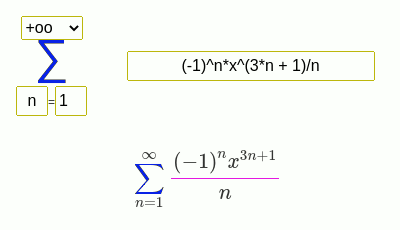
Seri toplamı bulma örnekleri
- Kuvvet serisinin toplamı
x^n/n
(x-1)^n
- Faktöriyel
1/2^(n!)
n^2/n!
x^n/n!
k!/(n!*(n+k)!)
- Flint Hills serisi
csc(n)^2/n^3
- Ters kareler serisi
1/n^2
1/n^4
1/n^6
- Harmonik seri
1/n
- Grandi serisi
(-1)^n
- Alternan seri
(-1)^(n + 1)/n
(n + 2)*(-1)^(n - 1)
(3*n - 1)/(-5)^n
(-1)^(n - 1)*n/(6*n - 5)
- Newton–Mercator serisi
(-1)^(n + 1)/n*x^n
- Seriyi yakınsama açısından incele
(3*n - 1)/(-5)^n
Seri toplamı hesaplayıcısı neler yapar?
Sigma işareti altındaki ifadeyi, ilk terimi, son terimi ya da toplamın limitini bulmak gerekiyorsa sonsuzluğu belirtirsiniz.
- Kısmi toplamları bulur
- Seri toplamının limiti
- Yakınsama ölçütlerine göre inceler:
- Iraksama
- Mutlak yakınsama. Yakınsayan seriler
- Koşullu yakınsama
- Tekdüze yakınsama
- Yakınsama için gerekli koşul
- Leibniz yakınsama ölçütü
- Weierstrass yakınsama ölçütü
- Abel yakınsama ölçütü
- Dirichlet yakınsama ölçütü
- Sınır karşılaştırma ölçütü
- Sınır karşılaştırma ölçütü
- Teleskopik ölçüt (Cauchy yoğunlaşma ölçütü)
- Cauchy–Maclaurin integral testi
- Karşılaştırma ölçütü
- Raabe–Duhamel ölçütü
- Destekler:
- Fonksiyonel seri:
x veya z değişkenleriyle
- Kuvvet serisi
- Taylor serisi
- Maclaurin serisi
- Fourier serisi
- Trigonometrik seri
- Laurent serisi
- Alternan seri / Alternan seri
- Ters kareler serisi
- Harmonik seri
- Grandi serisi
- Flint Hills serisi
- Kempner serisi
- Yakınsayan seri
- Iraksayan seri
- Pozitif seri
- Kısmi seri
- Diğerleri
- Fonksiyonel seri:
- Bulur:
- Serinin toplamını
- Serinin sayısal toplamı
- Serinin yakınsama hızı
- Kuvvet serisinin yakınsama yarıçapı
- Grafikler çizer:
- Kısmi toplamlar
- Serinin limiti
Hakkında daha fazla Seri toplamı
.
Yukarıda belirtilen örnekler ayrıca şunları içerir:
- mutlak değer veya mutlak değer: absolute(x) veya |x|
-
kare kökler sqrt(x),
kübik kökler cbrt(x) -
trigonometrik fonksiyonlar:
sinüs sin(x), kosinüs cos(x), tanjant tan(x), kotanjant ctan(x) - üstel fonksiyonlar ve üsler exp(x)
-
ters trigonometrik fonksiyonlar:
arksinüs asin(x), arkkosinüs acos(x), arktanjant atan(x), arkkotanjant acot(x) -
doğal logaritmalar ln(x),
ondalık logaritmalar log(x) -
hiperbolik fonksiyonlar:
hiperbolik sinüs sh(x), hiperbolik kosinüs ch(x), hiperbolik tanjant ve kotanjant tanh(x), ctanh(x) -
ters hiperbolik fonksiyonlar:
hiperbolik arksinüs asinh(x), hiperbolik arkkosinüs acosh(x), hiperbolik arktanjant atanh(x), hiperbolik arkkotanjant acoth(x) -
diğer trigonometrik ve hiperbolik fonksiyonlar:
sekant sec(x), kosekant csc(x), arksekant asec(x), arkkosekant acsc(x), hiperbolik sekant sech(x), hiperbolik kosekant csch(x), hiperbolik arksekant asech(x), hiperbolik arkkosekant acsch(x) -
yuvarlama fonksiyonları:
aşağı yuvarlama floor(x), yukarı yuvarlama ceiling(x) -
sayının işareti:
sign(x) -
olasılık teorisi için:
hata fonksiyonu erf(x) (olasılık integrali), Laplace fonksiyonu laplace(x) -
Şunun faktöriyeli x:
x! veya factorial(x) - Gamma fonksiyonu gamma(x)
- Lambert W fonksiyonu LambertW(x)
- Trigonometrik integraller: Si(x), Ci(x), Shi(x), Chi(x)
Girdi kuralları
Aşağıdaki işlemler yapılabilir
- 2*x
- - çarpma
- 3/x
- - bölme
- x^2
- - karesini alma
- x^3
- - küpünü alma
- x^5
- - üs alma
- x + 7
- - toplama
- x - 6
- - çıkarma
- Gerçek sayılar
- şu biçimde girin 7.5, değil 7,5
Sabitler
- pi
- - Pi sayısı
- e
- - doğal logaritmanın tabanı
- i
- - kompleks sayı
- oo
- - sonsuzluk sembolü
