Adım adım çift integral

Doğru integral çözümüyle grupta en sevilen olacaksın ❤️😊

Çift ∫∫dxdy integral türünü seçin

∫

∫∫
D

d d

Bölgeyi belirtin D:

Neler yapar?

Belirtilen çizgilerle sınırlı bölge üzerinde çift integrali hesaplar (burada), böylece integrasyon sınırlarını buna göre yerleştirir burada
Çift integral ile çizgilerle sınırlı şeklin alanını hesaplar
Tekrarlanan integralleri (sınırları bilinen) hesaplar
f(x, y) için çift integrali tekrarlı integral biçiminde yazar
Bir plakanın kütlesini çift integral yoluyla hesaplar
Tekrarlı integralde integrasyon sırasının değiştirilmesi (burada)
Uygulamanın anlamlı olduğu durumda kutupsal koordinatlar, kullanılır

Alan hesabı

Çizgilerle sınırlı şeklin alanını çift integral ile hesaplamak için integrandda yalnızca 1'i yerine koyun. Ayrıca aşağıdaki hesaplayıcıyı kullanabilirsiniz: Eğriler arasındaki şeklin alanı

Çift integral örnekleri

Kareli
```
8*x*y+9*x^2*y^2
```
Küplü
```
x^3+x*y^2
```
Sinüslü ve kare köklü
```
sin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2)
```
Doğrusal fonksiyon
```
2*x + y
```
Eğrilerle sınırlı şeklin alanını çift integralle bul
```
x^3*y^2
```
Çift integralde integrasyon sırasını değiştir
```
x^3*y^2
```
Eğrilerle sınırlı bölgede çift integral
```
x^3*y^2
```
Çift integralde integrasyon sınırlarını yerleştir
```
x^3*y^2
```
Polar sistemde çift integral
```
e^(x^2+y^2)
```
```
yln(1-x^2-y^2)/(x-sqrt(x^2+y^2))
```

D bölgesi nasıl tanımlanır?

D bölgesi çeşitli yollarla tanımlanabilir:

Eğri çizgilerle:
1. Çember
2. İki çember
3. Elips
4. Parabol
5. Diğerleri
Köşeler kullanılarak:
1. Üçgen
```
A(0, 1)
```
```
B(1, 0)
```
```
C(0, 0)
```
2. Kare
3. Dikdörtgen
ve — kadran

Eşitsizlik olarak

İntegrasyon bölgesi için kısıtı eşitsizlik biçiminde belirtin:

x > pi/2

-1/2 < y <= 3/2

x < sqrt(2)/2 + 1

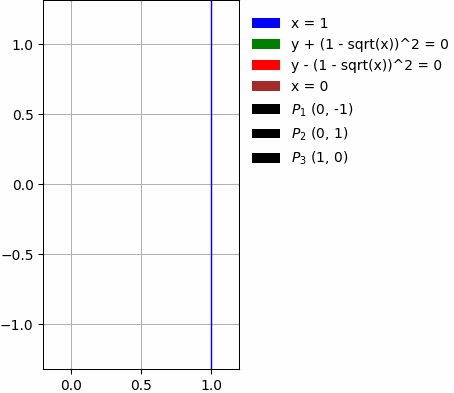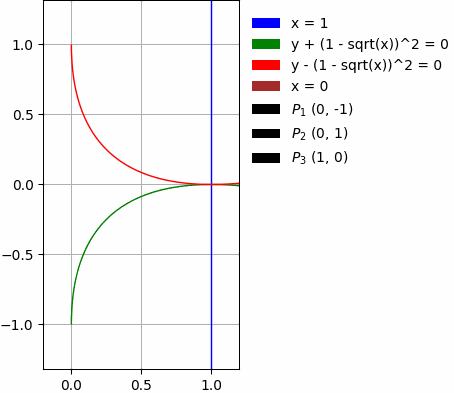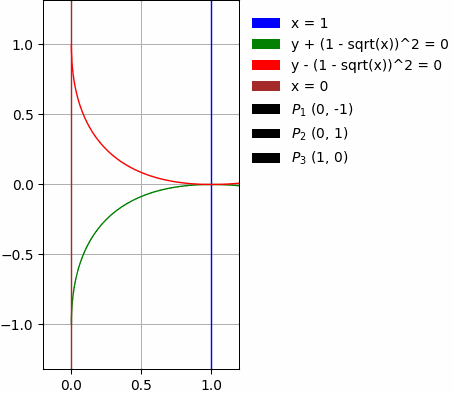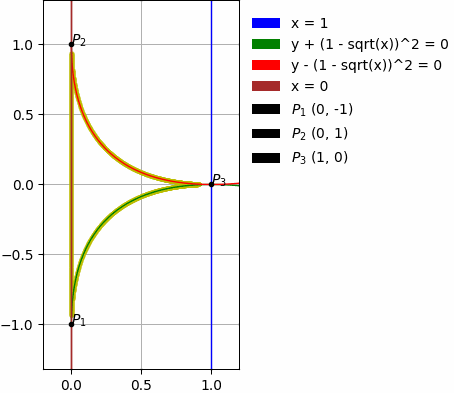
Yukarıda belirtilen örnekler ayrıca şunları içerir:

mutlak değer veya mutlak değer: absolute(x) veya |x|
kare kökler sqrt(x),
kübik kökler cbrt(x)
trigonometrik fonksiyonlar:
sinüs sin(x), kosinüs cos(x), tanjant tan(x), kotanjant ctan(x)
üstel fonksiyonlar ve üsler exp(x)
ters trigonometrik fonksiyonlar:
arksinüs asin(x), arkkosinüs acos(x), arktanjant atan(x), arkkotanjant acot(x)
doğal logaritmalar ln(x),
ondalık logaritmalar log(x)
hiperbolik fonksiyonlar:
hiperbolik sinüs sh(x), hiperbolik kosinüs ch(x), hiperbolik tanjant ve kotanjant tanh(x), ctanh(x)
ters hiperbolik fonksiyonlar:
hiperbolik arksinüs asinh(x), hiperbolik arkkosinüs acosh(x), hiperbolik arktanjant atanh(x), hiperbolik arkkotanjant acoth(x)
diğer trigonometrik ve hiperbolik fonksiyonlar:
sekant sec(x), kosekant csc(x), arksekant asec(x), arkkosekant acsc(x), hiperbolik sekant sech(x), hiperbolik kosekant csch(x), hiperbolik arksekant asech(x), hiperbolik arkkosekant acsch(x)
yuvarlama fonksiyonları:
aşağı yuvarlama floor(x), yukarı yuvarlama ceiling(x)
sayının işareti:
sign(x)
olasılık teorisi için:
hata fonksiyonu erf(x) (olasılık integrali), Laplace fonksiyonu laplace(x)
Şunun faktöriyeli x:
x! veya factorial(x)
Gamma fonksiyonu gamma(x)
Lambert W fonksiyonu LambertW(x)
Trigonometrik integraller: Si(x), Ci(x), Shi(x), Chi(x)

Girdi kuralları

Aşağıdaki işlemler yapılabilir

2*x: - çarpma
3/x: - bölme
x^2: - karesini alma
x^3: - küpünü alma
x^5: - üs alma
x + 7: - toplama
x - 6: - çıkarma
Gerçek sayılar: şu biçimde girin 7.5, değil 7,5

Sabitler

pi: - Pi sayısı
e: - doğal logaritmanın tabanı
i: - kompleks sayı
oo: - sonsuzluk sembolü

Bu örnekler, çift integralde üst ve alt sınırları girerken de uygulanabilir.

Diğer hesaplayıcılar