Mister Exam

Other calculators

Sum of series/ (1+sinx)/n^2

Sum of series (1+sinx)/n^2


∑
=

The solution

You have entered [src] 
  oo            
____            
\   `           
 \    1 + sin(x)
  \   ----------
  /        2    
 /        n     
/___,           
n = 1
$$\sum_{n=1}^{\infty} \frac{\sin{\left(x \right)} + 1}{n^{2}}$$ 
Sum((1 + sin(x))/n^2, (n, 1, oo))
The radius of convergence of the power series
Given number:
$$\frac{\sin{\left(x \right)} + 1}{n^{2}}$$
It is a series of species
$$a_{n} \left(c x - x_{0}\right)^{d n}$$
- power series.
The radius of convergence of a power series can be calculated by the formula:
$$R^{d} = \frac{x_{0} + \lim_{n \to \infty} \left|{\frac{a_{n}}{a_{n + 1}}}\right|}{c}$$
In this case
$$a_{n} = \frac{\sin{\left(x \right)} + 1}{n^{2}}$$
and
$$x_{0} = 0$$
,
$$d = 0$$
,
$$c = 1$$
then
$$1 = \lim_{n \to \infty}\left(\frac{\left(n + 1\right)^{2}}{n^{2}}\right)$$
Let's take the limit
we find
True

False
The answer [src] 
  2     2       
pi    pi *sin(x)
--- + ----------
 6        6
$$\frac{\pi^{2} \sin{\left(x \right)}}{6} + \frac{\pi^{2}}{6}$$ 
pi^2/6 + pi^2*sin(x)/6

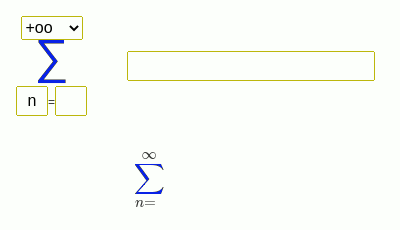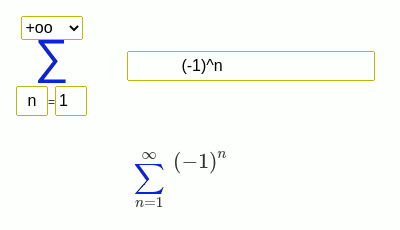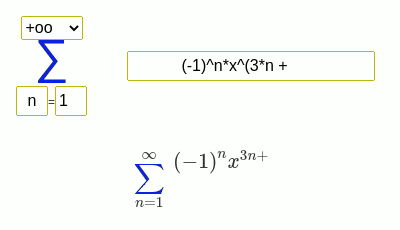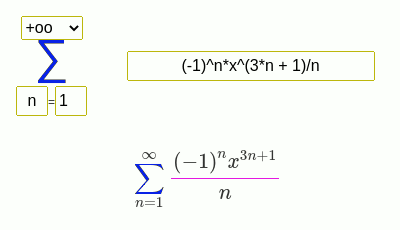
    Examples of finding the sum of a series

    © Mister Exam – Calculator