Sum of series n-2

The solution

You have entered [src]

  oo         
 __          
 \ `         
  )   (n - 2)
 /_,         
k = 1

$$\sum_{k=1}^{\infty} \left(n - 2\right)$$

Sum(n - 2, (k, 1, oo))

The radius of convergence of the power series

Given number:
$$n - 2$$
It is a series of species
$$a_{k} \left(c x - x_{0}\right)^{d k}$$
- power series.
The radius of convergence of a power series can be calculated by the formula:
$$R^{d} = \frac{x_{0} + \lim_{k \to \infty} \left|{\frac{a_{k}}{a_{k + 1}}}\right|}{c}$$
In this case
$$a_{k} = n - 2$$
and
$$x_{0} = 0$$
,
$$d = 0$$
,
$$c = 1$$
then
$$1 = \lim_{k \to \infty} 1$$
Let's take the limit
we find

True

False

The answer [src]

oo*(-2 + n)

$$\infty \left(n - 2\right)$$

oo*(-2 + n)

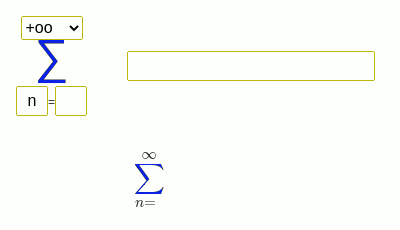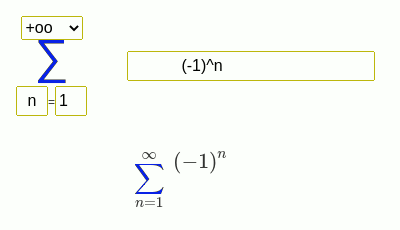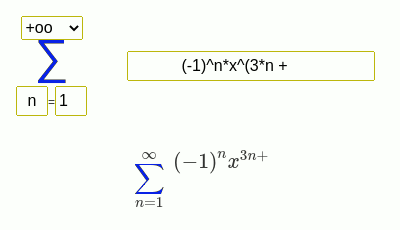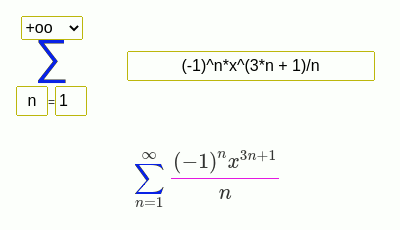
Examples of finding the sum of a series

The Sum of the Power Series
```
x^n/n
```
```
(x-1)^n
```
Factorial
```
1/2^(n!)
```
```
n^2/n!
```
```
x^n/n!
```
```
k!/(n!*(n+k)!)
```
Flint Hills Series
```
csc(n)^2/n^3
```
Basel problem
```
1/n^2
```
```
1/n^4
```
```
1/n^6
```
Harmonic series
```
1/n
```
Grandi's series
```
(-1)^n
```
Alternating series
```
(-1)^(n + 1)/n
```
```
(n + 2)*(-1)^(n - 1)
```
```
(3*n - 1)/(-5)^n
```
```
(-1)^(n - 1)*n/(6*n - 5)
```
Newton–Mercator series
```
(-1)^(n + 1)/n*x^n
```
Exam the series for convergence
```
(3*n - 1)/(-5)^n
```

Other calculators

How to use it?

Identical expressions

Similar expressions

Sum of series n-2

The solution

Examples of finding the sum of a series