Sum of series log^3
The solution
You have entered
[src]
oo ___ \ ` \ 3 / log (x) /__, n = 1
$$\sum_{n=1}^{\infty} \log{\left(x \right)}^{3}$$
Sum(log(x)^3, (n, 1, oo))
The radius of convergence of the power series
Given number:
$$\log{\left(x \right)}^{3}$$
It is a series of species
$$a_{n} \left(c x - x_{0}\right)^{d n}$$
- power series.
The radius of convergence of a power series can be calculated by the formula:
$$R^{d} = \frac{x_{0} + \lim_{n \to \infty} \left|{\frac{a_{n}}{a_{n + 1}}}\right|}{c}$$
In this case
$$a_{n} = \log{\left(x \right)}^{3}$$
and
$$x_{0} = 0$$
,
$$d = 0$$
,
$$c = 1$$
then
$$1 = \lim_{n \to \infty} 1$$
Let's take the limit
we find
$$\log{\left(x \right)}^{3}$$
It is a series of species
$$a_{n} \left(c x - x_{0}\right)^{d n}$$
- power series.
The radius of convergence of a power series can be calculated by the formula:
$$R^{d} = \frac{x_{0} + \lim_{n \to \infty} \left|{\frac{a_{n}}{a_{n + 1}}}\right|}{c}$$
In this case
$$a_{n} = \log{\left(x \right)}^{3}$$
and
$$x_{0} = 0$$
,
$$d = 0$$
,
$$c = 1$$
then
$$1 = \lim_{n \to \infty} 1$$
Let's take the limit
we find
True
False
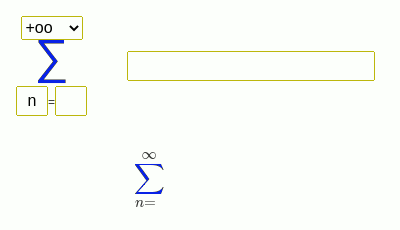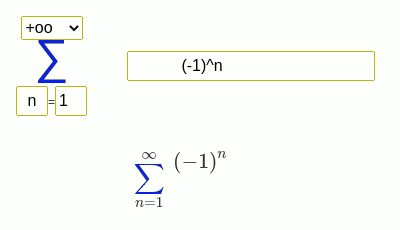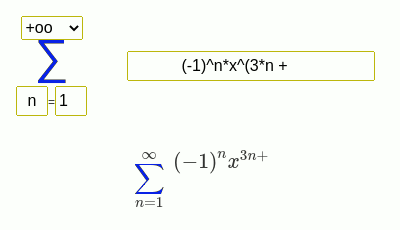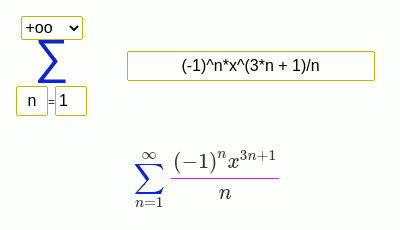
Examples of finding the sum of a series
- The Sum of the Power Series
x^n/n
(x-1)^n
- Factorial
1/2^(n!)
n^2/n!
x^n/n!
k!/(n!*(n+k)!)
- Flint Hills Series
csc(n)^2/n^3
- Basel problem
1/n^2
1/n^4
1/n^6
- Harmonic series
1/n
- Grandi's series
(-1)^n
- Alternating series
(-1)^(n + 1)/n
(n + 2)*(-1)^(n - 1)
(3*n - 1)/(-5)^n
(-1)^(n - 1)*n/(6*n - 5)
- Newton–Mercator series
(-1)^(n + 1)/n*x^n
- Exam the series for convergence
(3*n - 1)/(-5)^n

 (7^n-2^n)/14^n
(7^n-2^n)/14^n
 sin(sqrt(n^3-1)/(n^2+1))^2
sin(sqrt(n^3-1)/(n^2+1))^2
 ((n^2)/(9n^2-1))^2
((n^2)/(9n^2-1))^2