Limit of the function z^4
The solution
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
The graph
Other limits z→0, -oo, +oo, 1
$$\lim_{z \to -1^-} z^{4} = 1$$
More at z→-1 from the left
$$\lim_{z \to -1^+} z^{4} = 1$$
$$\lim_{z \to \infty} z^{4} = \infty$$
More at z→oo
$$\lim_{z \to 0^-} z^{4} = 0$$
More at z→0 from the left
$$\lim_{z \to 0^+} z^{4} = 0$$
More at z→0 from the right
$$\lim_{z \to 1^-} z^{4} = 1$$
More at z→1 from the left
$$\lim_{z \to 1^+} z^{4} = 1$$
More at z→1 from the right
$$\lim_{z \to -\infty} z^{4} = \infty$$
More at z→-oo
More at z→-1 from the left
$$\lim_{z \to -1^+} z^{4} = 1$$
$$\lim_{z \to \infty} z^{4} = \infty$$
More at z→oo
$$\lim_{z \to 0^-} z^{4} = 0$$
More at z→0 from the left
$$\lim_{z \to 0^+} z^{4} = 0$$
More at z→0 from the right
$$\lim_{z \to 1^-} z^{4} = 1$$
More at z→1 from the left
$$\lim_{z \to 1^+} z^{4} = 1$$
More at z→1 from the right
$$\lim_{z \to -\infty} z^{4} = \infty$$
More at z→-oo
One‐sided limits
[src]
4 lim z z->-1+
$$\lim_{z \to -1^+} z^{4}$$
1
$$1$$
= 1.0
4 lim z z->-1-
$$\lim_{z \to -1^-} z^{4}$$
1
$$1$$
= 1.0
= 1.0
The graph


![Limit of the function lim y = f(x) = z⁴ (z to the power of 4) at point x -> -1 and infinity - find and calculate with the detailed solution [THERE'S THE ANSWER!] z^4](/media/krcore-image-pods/176/b/99/86ccc7aa6e4564092a950b037a395.png)
 Limit of sin(17*x)/sin(12*x)
Limit of sin(17*x)/sin(12*x)
 Limit of log(x)/x
Limit of log(x)/x
 Limit of n^2
Limit of n^2
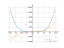 z^4
z^4