Mister Exam
Other calculators:
-
How to use it?
- Limit of the function:
-
Limit of -sin(x)+tan(x)
-
Limit of cos(x)*tan(5*x)
-
Limit of -1+sqrt(5)-sqrt(2)-2*x
-
Limit of ((-1+4*x)/(3+4*x))^(2+3*x)
- Derivative of:
-
9*x^2
- Integral of d{x}:
-
9*x^2
- Graphing y =:
-
9*x^2
-
Identical expressions
- nine *x^ two
- 9 multiply by x squared
- nine multiply by x to the power of two
- 9*x2
- 9*x²
- 9*x to the power of 2
- 9x^2
- 9x2
-
Similar expressions
- 7+6*x+9*x^2/2
- (2-x+4*x^2)/(-5+x+9*x^2)
- (-8+27*x^3)/(-4+9*x^2)
Limit of the function 9*x^2
The solution
You have entered
[src]
/ 2\ lim \9*x / x->oo
$$\lim_{x \to \infty}\left(9 x^{2}\right)$$
Limit(9*x^2, x, oo, dir='-')
Detail solution
Let's take the limit
$$\lim_{x \to \infty}\left(9 x^{2}\right)$$
Let's divide numerator and denominator by x^2:
$$\lim_{x \to \infty}\left(9 x^{2}\right)$$ =
$$\lim_{x \to \infty} \frac{1}{\frac{1}{9} \frac{1}{x^{2}}}$$
Do Replacement
$$u = \frac{1}{x}$$
then
$$\lim_{x \to \infty} \frac{1}{\frac{1}{9} \frac{1}{x^{2}}} = \lim_{u \to 0^+}\left(\frac{9}{u^{2}}\right)$$
=
$$\frac{9}{0} = \infty$$
The final answer:
$$\lim_{x \to \infty}\left(9 x^{2}\right) = \infty$$
$$\lim_{x \to \infty}\left(9 x^{2}\right)$$
Let's divide numerator and denominator by x^2:
$$\lim_{x \to \infty}\left(9 x^{2}\right)$$ =
$$\lim_{x \to \infty} \frac{1}{\frac{1}{9} \frac{1}{x^{2}}}$$
Do Replacement
$$u = \frac{1}{x}$$
then
$$\lim_{x \to \infty} \frac{1}{\frac{1}{9} \frac{1}{x^{2}}} = \lim_{u \to 0^+}\left(\frac{9}{u^{2}}\right)$$
=
$$\frac{9}{0} = \infty$$
The final answer:
$$\lim_{x \to \infty}\left(9 x^{2}\right) = \infty$$
Lopital's rule
There is no sense to apply Lopital's rule to this function since there is no indeterminateness of 0/0 or oo/oo type
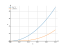
The graph
Other limits x→0, -oo, +oo, 1
$$\lim_{x \to \infty}\left(9 x^{2}\right) = \infty$$
$$\lim_{x \to 0^-}\left(9 x^{2}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(9 x^{2}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-}\left(9 x^{2}\right) = 9$$
More at x→1 from the left
$$\lim_{x \to 1^+}\left(9 x^{2}\right) = 9$$
More at x→1 from the right
$$\lim_{x \to -\infty}\left(9 x^{2}\right) = \infty$$
More at x→-oo
$$\lim_{x \to 0^-}\left(9 x^{2}\right) = 0$$
More at x→0 from the left
$$\lim_{x \to 0^+}\left(9 x^{2}\right) = 0$$
More at x→0 from the right
$$\lim_{x \to 1^-}\left(9 x^{2}\right) = 9$$
More at x→1 from the left
$$\lim_{x \to 1^+}\left(9 x^{2}\right) = 9$$
More at x→1 from the right
$$\lim_{x \to -\infty}\left(9 x^{2}\right) = \infty$$
More at x→-oo
The graph