Mister Exam

Other calculators:

log(x)*sin(x)
Limit of the function/ log(x)*sin(x)

Limit of the function log(x)*sin(x)

at →
v

For end points:

The graph:

from to

Piecewise:

The solution

You have entered [src] 
 lim (log(x)*sin(x))
x->0+
lim⁡x→0+(log⁡(x)sin⁡(x))\lim_{x \to 0^+}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) 
Limit(log(x)*sin(x), x, 0)
Lopital's rule
We have indeterminateness of type
0/0,

i.e. limit for the numerator is
lim⁡x→0+sin⁡(x)=0\lim_{x \to 0^+} \sin{\left(x \right)} = 0
and limit for the denominator is
lim⁡x→0+1log⁡(x)=0\lim_{x \to 0^+} \frac{1}{\log{\left(x \right)}} = 0
Let's take derivatives of the numerator and denominator until we eliminate indeterninateness.
lim⁡x→0+(log⁡(x)sin⁡(x))\lim_{x \to 0^+}\left(\log{\left(x \right)} \sin{\left(x \right)}\right)
=
lim⁡x→0+(ddxsin⁡(x)ddx1log⁡(x))\lim_{x \to 0^+}\left(\frac{\frac{d}{d x} \sin{\left(x \right)}}{\frac{d}{d x} \frac{1}{\log{\left(x \right)}}}\right)
=
lim⁡x→0+(−xlog⁡(x)2cos⁡(x))\lim_{x \to 0^+}\left(- x \log{\left(x \right)}^{2} \cos{\left(x \right)}\right)
=
lim⁡x→0+(−xlog⁡(x)2cos⁡(x))\lim_{x \to 0^+}\left(- x \log{\left(x \right)}^{2} \cos{\left(x \right)}\right)
=
00
It can be seen that we have applied Lopital's rule (we have taken derivatives with respect to the numerator and denominator) 1 time(s)
The graph
02468-8-6-4-2-10105-5
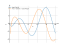
Plot the graph
Other limits x→0, -oo, +oo, 1
lim⁡x→0−(log⁡(x)sin⁡(x))=0\lim_{x \to 0^-}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = 0
More at x→0 from the left
lim⁡x→0+(log⁡(x)sin⁡(x))=0\lim_{x \to 0^+}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = 0
lim⁡x→∞(log⁡(x)sin⁡(x))=⟨−∞,∞⟩\lim_{x \to \infty}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = \left\langle -\infty, \infty\right\rangle
More at x→oo
lim⁡x→1−(log⁡(x)sin⁡(x))=0\lim_{x \to 1^-}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = 0
More at x→1 from the left
lim⁡x→1+(log⁡(x)sin⁡(x))=0\lim_{x \to 1^+}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = 0
More at x→1 from the right
lim⁡x→−∞(log⁡(x)sin⁡(x))=⟨−∞,∞⟩\lim_{x \to -\infty}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) = \left\langle -\infty, \infty\right\rangle
More at x→-oo
Rapid solution [src] 
0
00
Expand and simplify
One‐sided limits [src] 
 lim (log(x)*sin(x))
x->0+
lim⁡x→0+(log⁡(x)sin⁡(x))\lim_{x \to 0^+}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) 
0
00 
= -0.001891842431455
 lim (log(x)*sin(x))
x->0-
lim⁡x→0−(log⁡(x)sin⁡(x))\lim_{x \to 0^-}\left(\log{\left(x \right)} \sin{\left(x \right)}\right) 
0
00 
= (0.001880931816114 - 0.000776106987906943j)
= (0.001880931816114 - 0.000776106987906943j)
Numerical answer [src] 
-0.001891842431455
-0.001891842431455
The graph
Limit of the function log(x)*sin(x)
    © Mister Exam – Calculator