Integral of x/x√1-ln^2x dx
The solution
Detail solution
-
Integrate term-by-term:
-
The integral of a constant times a function is the constant times the integral of the function:
∫(−log(x)2)dx=−∫log(x)2dx
-
Let u=log(x).
Then let du=xdx and substitute du:
∫u2eudu
-
Use integration by parts:
∫udv=uv−∫vdu
Let u(u)=u2 and let dv(u)=eu.
Then du(u)=2u.
To find v(u):
-
The integral of the exponential function is itself.
∫eudu=eu
Now evaluate the sub-integral.
-
Use integration by parts:
∫udv=uv−∫vdu
Let u(u)=2u and let dv(u)=eu.
Then du(u)=2.
To find v(u):
-
The integral of the exponential function is itself.
∫eudu=eu
Now evaluate the sub-integral.
-
The integral of a constant times a function is the constant times the integral of the function:
∫2eudu=2∫eudu
-
The integral of the exponential function is itself.
∫eudu=eu
So, the result is: 2eu
Now substitute u back in:
xlog(x)2−2xlog(x)+2x
So, the result is: −xlog(x)2+2xlog(x)−2x
-
The integral of a constant times a function is the constant times the integral of the function:
∫x1xdx=∫xxdx
-
Don't know the steps in finding this integral.
But the integral is
So, the result is: x
The result is: −xlog(x)2+2xlog(x)−x
-
Now simplify:
x(−log(x)2+2log(x)−1)
-
Add the constant of integration:
x(−log(x)2+2log(x)−1)+constant
The answer is:
x(−log(x)2+2log(x)−1)+constant
The answer (Indefinite)
[src]
/
|
| / ___ \
| |x*\/ 1 2 | 2
| |------- - log (x)| dx = C - x - x*log (x) + 2*x*log(x)
| \ x /
|
/
x−x((logx)2−2logx+2)
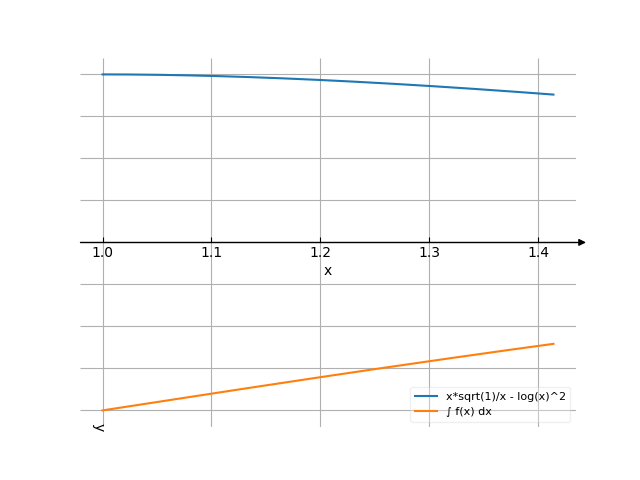
The graph
___ ___ 2/ ___\ ___ / ___\
1 - \/ 2 - \/ 2 *log \\/ 2 / + 2*\/ 2 *log\\/ 2 /
−223(log2)2−4log2−223+4
=
___ ___ 2/ ___\ ___ / ___\
1 - \/ 2 - \/ 2 *log \\/ 2 / + 2*\/ 2 *log\\/ 2 /
−2−2log(2)2+22log(2)+1
Use the examples entering the upper and lower limits of integration.

![Find the integral of y = f(x) = x/x√1-ln²x dx (x divide by x√1 minus ln squared x) - with detailed solution [THERE'S THE ANSWER!] x/x√1-ln^2x](/media/krcore-image-pods/176/hash/indefinite/7/15/a0a76f8b70fb2f6c9806a88c997a9.png)
 Integral of x*dx/sqrt(1-x^2)
Integral of x*dx/sqrt(1-x^2)
 Integral of x^4/(1+x^2)
Integral of x^4/(1+x^2)
 Integral of x^5/(x^2+1)
Integral of x^5/(x^2+1)
 Integral of (sinx+cosx)dx
Integral of (sinx+cosx)dx