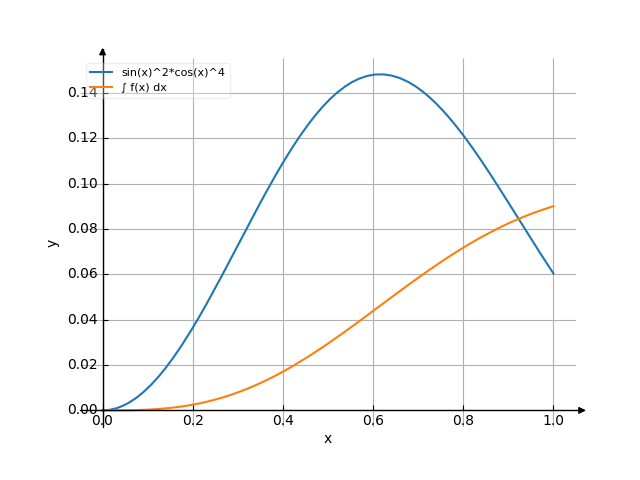
Integral of sin^2xcos^4x dx

The solution

You have entered [src]

  1                   
  /                   
 |                    
 |     2       4      
 |  sin (x)*cos (x) dx
 |                    
/                     
0

$$\int\limits_{0}^{1} \sin^{2}{\left(x \right)} \cos^{4}{\left(x \right)}\, dx$$

Integral(sin(x)^2*cos(x)^4, (x, 0, 1))

Detail solution

Rewrite the integrand:

$\sin^{2}{\left(x \right)} \cos^{4}{\left(x \right)} = \left(\frac{1}{2} - \frac{\cos{\left(2 x \right)}}{2}\right) \left(\frac{\cos{\left(2 x \right)}}{2} + \frac{1}{2}\right)^{2}$
There are multiple ways to do this integral.
Method #1
1. Let $u = 2 x$ .
  
  Then let $du = 2 dx$ and substitute $du$ :
  
  $\int \left(- \frac{\cos^{3}{\left(u \right)}}{16} - \frac{\cos^{2}{\left(u \right)}}{16} + \frac{\cos{\left(u \right)}}{16} + \frac{1}{16}\right)\, du$
  1. Integrate term-by-term:
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \left(- \frac{\cos^{3}{\left(u \right)}}{16}\right)\, du = - \frac{\int \cos^{3}{\left(u \right)}\, du}{16}$
      
      Rewrite the integrand:
      
      $\cos^{3}{\left(u \right)} = \left(1 - \sin^{2}{\left(u \right)}\right) \cos{\left(u \right)}$
      
      Let $u = \sin{\left(u \right)}$ .
      
      Then let $du = \cos{\left(u \right)} du$ and substitute $du$ :
      
      $\int \left(1 - u^{2}\right)\, du$
      
      Integrate term-by-term:
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int 1\, du = u$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \left(- u^{2}\right)\, du = - \int u^{2}\, du$
      
      The integral of $u^{n}$ is $\frac{u^{n + 1}}{n + 1}$ when $n \neq -1$ :
      
      $\int u^{2}\, du = \frac{u^{3}}{3}$
      
      So, the result is: $- \frac{u^{3}}{3}$
      
      The result is: $- \frac{u^{3}}{3} + u$
      
      Now substitute $u$ back in:
      
      $- \frac{\sin^{3}{\left(u \right)}}{3} + \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin^{3}{\left(u \right)}}{48} - \frac{\sin{\left(u \right)}}{16}$
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \left(- \frac{\cos^{2}{\left(u \right)}}{16}\right)\, du = - \frac{\int \cos^{2}{\left(u \right)}\, du}{16}$
      
      Rewrite the integrand:
      
      $\cos^{2}{\left(u \right)} = \frac{\cos{\left(2 u \right)}}{2} + \frac{1}{2}$
      
      Integrate term-by-term:
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(2 u \right)}}{2}\, du = \frac{\int \cos{\left(2 u \right)}\, du}{2}$
      
      Let $u = 2 u$ .
      
      Then let $du = 2 du$ and substitute $\frac{du}{2}$ :
      
      $\int \frac{\cos{\left(u \right)}}{4}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{2}\, du = \frac{\int \cos{\left(u \right)}\, du}{2}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{2}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(2 u \right)}}{2}$
      
      So, the result is: $\frac{\sin{\left(2 u \right)}}{4}$
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{2}\, du = \frac{u}{2}$
      
      The result is: $\frac{u}{2} + \frac{\sin{\left(2 u \right)}}{4}$
      
      So, the result is: $- \frac{u}{32} - \frac{\sin{\left(2 u \right)}}{64}$
    1. The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{16}\, du = \frac{\int \cos{\left(u \right)}\, du}{16}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{16}$
    1. The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{16}\, du = \frac{u}{16}$
    The result is: $\frac{u}{32} - \frac{\sin{\left(2 u \right)}}{64} + \frac{\sin^{3}{\left(u \right)}}{48}$
  Now substitute $u$ back in:
  
  $\frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}$
Method #2
1. Rewrite the integrand:
  
  $\left(\frac{1}{2} - \frac{\cos{\left(2 x \right)}}{2}\right) \left(\frac{\cos{\left(2 x \right)}}{2} + \frac{1}{2}\right)^{2} = - \frac{\cos^{3}{\left(2 x \right)}}{8} - \frac{\cos^{2}{\left(2 x \right)}}{8} + \frac{\cos{\left(2 x \right)}}{8} + \frac{1}{8}$
2. Integrate term-by-term:
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{\cos^{3}{\left(2 x \right)}}{8}\right)\, dx = - \frac{\int \cos^{3}{\left(2 x \right)}\, dx}{8}$
    1. Rewrite the integrand:
      
      $\cos^{3}{\left(2 x \right)} = \left(1 - \sin^{2}{\left(2 x \right)}\right) \cos{\left(2 x \right)}$
    2. Let $u = \sin{\left(2 x \right)}$ .
      
      Then let $du = 2 \cos{\left(2 x \right)} dx$ and substitute $du$ :
      
      $\int \left(\frac{1}{2} - \frac{u^{2}}{2}\right)\, du$
      
      Integrate term-by-term:
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{2}\, du = \frac{u}{2}$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \left(- \frac{u^{2}}{2}\right)\, du = - \frac{\int u^{2}\, du}{2}$
      
      The integral of $u^{n}$ is $\frac{u^{n + 1}}{n + 1}$ when $n \neq -1$ :
      
      $\int u^{2}\, du = \frac{u^{3}}{3}$
      
      So, the result is: $- \frac{u^{3}}{6}$
      
      The result is: $- \frac{u^{3}}{6} + \frac{u}{2}$
      
      Now substitute $u$ back in:
      
      $- \frac{\sin^{3}{\left(2 x \right)}}{6} + \frac{\sin{\left(2 x \right)}}{2}$
    So, the result is: $\frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(2 x \right)}}{16}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{\cos^{2}{\left(2 x \right)}}{8}\right)\, dx = - \frac{\int \cos^{2}{\left(2 x \right)}\, dx}{8}$
    1. Rewrite the integrand:
      
      $\cos^{2}{\left(2 x \right)} = \frac{\cos{\left(4 x \right)}}{2} + \frac{1}{2}$
    2. Integrate term-by-term:
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(4 x \right)}}{2}\, dx = \frac{\int \cos{\left(4 x \right)}\, dx}{2}$
      
      Let $u = 4 x$ .
      
      Then let $du = 4 dx$ and substitute $\frac{du}{4}$ :
      
      $\int \frac{\cos{\left(u \right)}}{16}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{4}\, du = \frac{\int \cos{\left(u \right)}\, du}{4}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{4}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(4 x \right)}}{4}$
      
      So, the result is: $\frac{\sin{\left(4 x \right)}}{8}$
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{2}\, dx = \frac{x}{2}$
      
      The result is: $\frac{x}{2} + \frac{\sin{\left(4 x \right)}}{8}$
    So, the result is: $- \frac{x}{16} - \frac{\sin{\left(4 x \right)}}{64}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \frac{\cos{\left(2 x \right)}}{8}\, dx = \frac{\int \cos{\left(2 x \right)}\, dx}{8}$
    1. Let $u = 2 x$ .
      
      Then let $du = 2 dx$ and substitute $\frac{du}{2}$ :
      
      $\int \frac{\cos{\left(u \right)}}{4}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{2}\, du = \frac{\int \cos{\left(u \right)}\, du}{2}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{2}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(2 x \right)}}{2}$
    So, the result is: $\frac{\sin{\left(2 x \right)}}{16}$
  1. The integral of a constant is the constant times the variable of integration:
    
    $\int \frac{1}{8}\, dx = \frac{x}{8}$
  The result is: $\frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}$
Method #3
1. Rewrite the integrand:
  
  $\left(\frac{1}{2} - \frac{\cos{\left(2 x \right)}}{2}\right) \left(\frac{\cos{\left(2 x \right)}}{2} + \frac{1}{2}\right)^{2} = - \frac{\cos^{3}{\left(2 x \right)}}{8} - \frac{\cos^{2}{\left(2 x \right)}}{8} + \frac{\cos{\left(2 x \right)}}{8} + \frac{1}{8}$
2. Integrate term-by-term:
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{\cos^{3}{\left(2 x \right)}}{8}\right)\, dx = - \frac{\int \cos^{3}{\left(2 x \right)}\, dx}{8}$
    1. Rewrite the integrand:
      
      $\cos^{3}{\left(2 x \right)} = \left(1 - \sin^{2}{\left(2 x \right)}\right) \cos{\left(2 x \right)}$
    2. Let $u = \sin{\left(2 x \right)}$ .
      
      Then let $du = 2 \cos{\left(2 x \right)} dx$ and substitute $du$ :
      
      $\int \left(\frac{1}{2} - \frac{u^{2}}{2}\right)\, du$
      
      Integrate term-by-term:
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{2}\, du = \frac{u}{2}$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \left(- \frac{u^{2}}{2}\right)\, du = - \frac{\int u^{2}\, du}{2}$
      
      The integral of $u^{n}$ is $\frac{u^{n + 1}}{n + 1}$ when $n \neq -1$ :
      
      $\int u^{2}\, du = \frac{u^{3}}{3}$
      
      So, the result is: $- \frac{u^{3}}{6}$
      
      The result is: $- \frac{u^{3}}{6} + \frac{u}{2}$
      
      Now substitute $u$ back in:
      
      $- \frac{\sin^{3}{\left(2 x \right)}}{6} + \frac{\sin{\left(2 x \right)}}{2}$
    So, the result is: $\frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(2 x \right)}}{16}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \left(- \frac{\cos^{2}{\left(2 x \right)}}{8}\right)\, dx = - \frac{\int \cos^{2}{\left(2 x \right)}\, dx}{8}$
    1. Rewrite the integrand:
      
      $\cos^{2}{\left(2 x \right)} = \frac{\cos{\left(4 x \right)}}{2} + \frac{1}{2}$
    2. Integrate term-by-term:
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(4 x \right)}}{2}\, dx = \frac{\int \cos{\left(4 x \right)}\, dx}{2}$
      
      Let $u = 4 x$ .
      
      Then let $du = 4 dx$ and substitute $\frac{du}{4}$ :
      
      $\int \frac{\cos{\left(u \right)}}{16}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{4}\, du = \frac{\int \cos{\left(u \right)}\, du}{4}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{4}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(4 x \right)}}{4}$
      
      So, the result is: $\frac{\sin{\left(4 x \right)}}{8}$
      
      The integral of a constant is the constant times the variable of integration:
      
      $\int \frac{1}{2}\, dx = \frac{x}{2}$
      
      The result is: $\frac{x}{2} + \frac{\sin{\left(4 x \right)}}{8}$
    So, the result is: $- \frac{x}{16} - \frac{\sin{\left(4 x \right)}}{64}$
  1. The integral of a constant times a function is the constant times the integral of the function:
    
    $\int \frac{\cos{\left(2 x \right)}}{8}\, dx = \frac{\int \cos{\left(2 x \right)}\, dx}{8}$
    1. Let $u = 2 x$ .
      
      Then let $du = 2 dx$ and substitute $\frac{du}{2}$ :
      
      $\int \frac{\cos{\left(u \right)}}{4}\, du$
      
      The integral of a constant times a function is the constant times the integral of the function:
      
      $\int \frac{\cos{\left(u \right)}}{2}\, du = \frac{\int \cos{\left(u \right)}\, du}{2}$
      
      The integral of cosine is sine:
      
      $\int \cos{\left(u \right)}\, du = \sin{\left(u \right)}$
      
      So, the result is: $\frac{\sin{\left(u \right)}}{2}$
      
      Now substitute $u$ back in:
      
      $\frac{\sin{\left(2 x \right)}}{2}$
    So, the result is: $\frac{\sin{\left(2 x \right)}}{16}$
  1. The integral of a constant is the constant times the variable of integration:
    
    $\int \frac{1}{8}\, dx = \frac{x}{8}$
  The result is: $\frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}$
Add the constant of integration:

$\frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}+ \mathrm{constant}$

The answer is:

$\frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}+ \mathrm{constant}$

The answer (Indefinite) [src]

  /                                                  
 |                                             3     
 |    2       4             sin(4*x)   x    sin (2*x)
 | sin (x)*cos (x) dx = C - -------- + -- + ---------
 |                             64      16       48   
/

$$\int \sin^{2}{\left(x \right)} \cos^{4}{\left(x \right)}\, dx = C + \frac{x}{16} + \frac{\sin^{3}{\left(2 x \right)}}{48} - \frac{\sin{\left(4 x \right)}}{64}$$

Simplify

The graph

Plot the graph f(x)

The answer [src]

        5                                3          
1    cos (1)*sin(1)   cos(1)*sin(1)   cos (1)*sin(1)
-- - -------------- + ------------- + --------------
16         6                16              24

$$- \frac{\sin{\left(1 \right)} \cos^{5}{\left(1 \right)}}{6} + \frac{\sin{\left(1 \right)} \cos^{3}{\left(1 \right)}}{24} + \frac{\sin{\left(1 \right)} \cos{\left(1 \right)}}{16} + \frac{1}{16}$$

        5                                3          
1    cos (1)*sin(1)   cos(1)*sin(1)   cos (1)*sin(1)
-- - -------------- + ------------- + --------------
16         6                16              24

$$- \frac{\sin{\left(1 \right)} \cos^{5}{\left(1 \right)}}{6} + \frac{\sin{\left(1 \right)} \cos^{3}{\left(1 \right)}}{24} + \frac{\sin{\left(1 \right)} \cos{\left(1 \right)}}{16} + \frac{1}{16}$$

Упростить

Numerical answer [src]

0.0899881003364571

0.0899881003364571

The graph

Use the examples entering the upper and lower limits of integration.

Other calculators

How to use it?

Identical expressions

Similar expressions

Integral of sin^2xcos^4x dx

Limits of integration:

The graph:

Piecewise:

The solution

Method #1

Method #2

Method #3