Mister Exam
Other calculators
- Improper integral
- Double Integral
- Triple Integral
- Curvilinear integral
- Derivative Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Integral of d{x}:
-
Integral of x^e
-
Integral of sin(x²)
-
Integral of 1/(x³+1)
- Integral of ln(x+(1+x^2)^(1/2))
-
Identical expressions
- one /(sqrt(e^(six *x)- four))
- 1 divide by ( square root of (e to the power of (6 multiply by x) minus 4))
- one divide by ( square root of (e to the power of (six multiply by x) minus four))
- 1/(√(e^(6*x)-4))
- 1/(sqrt(e(6*x)-4))
- 1/sqrte6*x-4
- 1/(sqrt(e^(6x)-4))
- 1/(sqrt(e(6x)-4))
- 1/sqrte6x-4
- 1/sqrte^6x-4
- 1 divide by (sqrt(e^(6*x)-4))
- 1/(sqrt(e^(6*x)-4))dx
-
Similar expressions
- 1/(sqrt(e^(6*x)+4))
Integral of 1/(sqrt(e^(6*x)-4)) dx
The solution
You have entered
[src]
1 / | | 1 | 1*------------- dx | __________ | / 6*x | \/ e - 4 | / 0
$$\int\limits_{0}^{1} 1 \cdot \frac{1}{\sqrt{e^{6 x} - 4}}\, dx$$
Integral(1/sqrt(E^(6*x) - 1*4), (x, 0, 1))
The answer (Indefinite)
[src]
$${{\arctan \left({{\sqrt{e^{6\,x}-4}}\over{2}}\right)}\over{6}}$$
The graph
The answer
[src]
/ _________\
| / 6 | / ___\
|\/ -4 + e | |\/ 3 |
atan|------------| I*atanh|-----|
\ 2 / \ 2 /
------------------ - --------------
6 6
$${{\arctan \left({{\sqrt{e^6-4}}\over{2}}\right)-i\,{\rm atanh}\;
\left({{\sqrt{3}}\over{2}}\right)}\over{6}}$$
=
=
/ _________\
| / 6 | / ___\
|\/ -4 + e | |\/ 3 |
atan|------------| I*atanh|-----|
\ 2 / \ 2 /
------------------ - --------------
6 6
$$\frac{\operatorname{atan}{\left(\frac{\sqrt{-4 + e^{6}}}{2} \right)}}{6} - \frac{i \operatorname{atanh}{\left(\frac{\sqrt{3}}{2} \right)}}{6}$$
Numerical answer
[src]
(0.21812576599571 - 0.265385439732854j)
(0.21812576599571 - 0.265385439732854j)
The graph
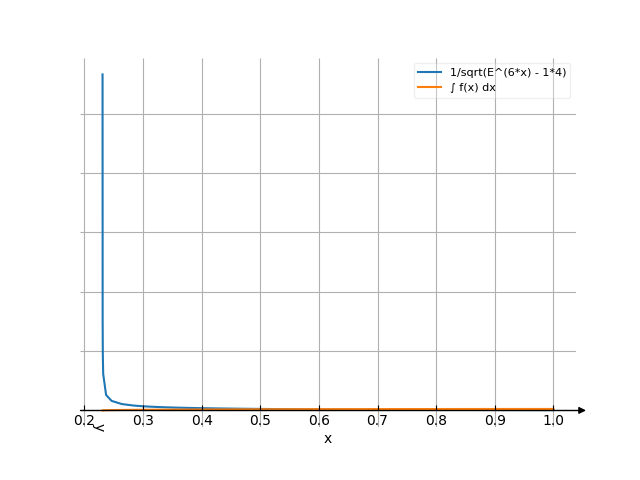
Use the examples entering the upper and lower limits of integration.