Integral of 3e^(3x) dx
The solution
Detail solution
-
The integral of a constant times a function is the constant times the integral of the function:
-
Don't know the steps in finding this integral.
But the integral is
So, the result is:
-
-
Add the constant of integration:
The answer is:
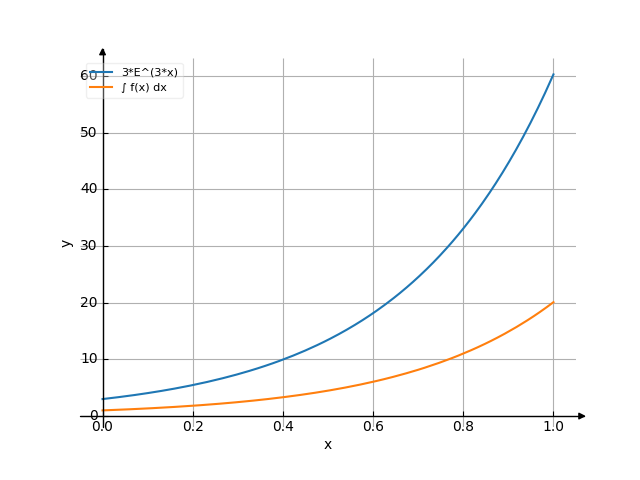
The graph
The answer
[src]
3 -1 + e
$$3\,\left({{e^3}\over{3}}-{{1}\over{3}}\right)$$
=
=
3 -1 + e
$$-1 + e^{3}$$
The graph
Use the examples entering the upper and lower limits of integration.

![Find the integral of y = f(x) = 3e^(3x) dx (3e to the power of (3x)) - with detailed solution [THERE'S THE ANSWER!] 3e^(3x)](/media/krcore-image-pods/176/hash/indefinite/d/3b/20cfeb76417f14147e159e86008ac.png)
 Integral of log(3x-2)
Integral of log(3x-2)
 Integral of 3e^(3x)
Integral of 3e^(3x)
 Integral of 12dx
Integral of 12dx
 Integral of sin^7(x)*cos^2(x)
Integral of sin^7(x)*cos^2(x)
 3e^(3x)
3e^(3x)