(x+2)^3<1 inequation
The solution
Detail solution
Given the inequality:
$$\left(x + 2\right)^{3} < 1$$
To solve this inequality, we must first solve the corresponding equation:
$$\left(x + 2\right)^{3} = 1$$
Solve:
Given the equation
$$\left(x + 2\right)^{3} = 1$$
Because equation degree is equal to = 3 - does not contain even numbers in the numerator, then
the equation has single real root.
Get the root 3-th degree of the equation sides:
We get:
$$\sqrt[3]{\left(x + 2\right)^{3}} = \sqrt[3]{1}$$
or
$$x + 2 = 1$$
Move free summands (without x)
from left part to right part, we given:
$$x = -1$$
We get the answer: x = -1
All other 2 root(s) is the complex numbers.
do replacement:
$$z = x + 2$$
then the equation will be the:
$$z^{3} = 1$$
Any complex number can presented so:
$$z = r e^{i p}$$
substitute to the equation
$$r^{3} e^{3 i p} = 1$$
where
$$r = 1$$
- the magnitude of the complex number
Substitute r:
$$e^{3 i p} = 1$$
Using Euler’s formula, we find roots for p
$$i \sin{\left(3 p \right)} + \cos{\left(3 p \right)} = 1$$
so
$$\cos{\left(3 p \right)} = 1$$
and
$$\sin{\left(3 p \right)} = 0$$
then
$$p = \frac{2 \pi N}{3}$$
where N=0,1,2,3,...
Looping through the values of N and substituting p into the formula for z
Consequently, the solution will be for z:
$$z_{1} = 1$$
$$z_{2} = - \frac{1}{2} - \frac{\sqrt{3} i}{2}$$
$$z_{3} = - \frac{1}{2} + \frac{\sqrt{3} i}{2}$$
do backward replacement
$$z = x + 2$$
$$x = z - 2$$
$$x_{1} = -1$$
$$x_{1} = -1$$
This roots
$$x_{1} = -1$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$-1 + - \frac{1}{10}$$
=
$$- \frac{11}{10}$$
substitute to the expression
$$\left(x + 2\right)^{3} < 1$$
$$\left(- \frac{11}{10} + 2\right)^{3} < 1$$
the solution of our inequality is:
$$x < -1$$
$$\left(x + 2\right)^{3} < 1$$
To solve this inequality, we must first solve the corresponding equation:
$$\left(x + 2\right)^{3} = 1$$
Solve:
Given the equation
$$\left(x + 2\right)^{3} = 1$$
Because equation degree is equal to = 3 - does not contain even numbers in the numerator, then
the equation has single real root.
Get the root 3-th degree of the equation sides:
We get:
$$\sqrt[3]{\left(x + 2\right)^{3}} = \sqrt[3]{1}$$
or
$$x + 2 = 1$$
Move free summands (without x)
from left part to right part, we given:
$$x = -1$$
We get the answer: x = -1
All other 2 root(s) is the complex numbers.
do replacement:
$$z = x + 2$$
then the equation will be the:
$$z^{3} = 1$$
Any complex number can presented so:
$$z = r e^{i p}$$
substitute to the equation
$$r^{3} e^{3 i p} = 1$$
where
$$r = 1$$
- the magnitude of the complex number
Substitute r:
$$e^{3 i p} = 1$$
Using Euler’s formula, we find roots for p
$$i \sin{\left(3 p \right)} + \cos{\left(3 p \right)} = 1$$
so
$$\cos{\left(3 p \right)} = 1$$
and
$$\sin{\left(3 p \right)} = 0$$
then
$$p = \frac{2 \pi N}{3}$$
where N=0,1,2,3,...
Looping through the values of N and substituting p into the formula for z
Consequently, the solution will be for z:
$$z_{1} = 1$$
$$z_{2} = - \frac{1}{2} - \frac{\sqrt{3} i}{2}$$
$$z_{3} = - \frac{1}{2} + \frac{\sqrt{3} i}{2}$$
do backward replacement
$$z = x + 2$$
$$x = z - 2$$
$$x_{1} = -1$$
$$x_{1} = -1$$
This roots
$$x_{1} = -1$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$-1 + - \frac{1}{10}$$
=
$$- \frac{11}{10}$$
substitute to the expression
$$\left(x + 2\right)^{3} < 1$$
$$\left(- \frac{11}{10} + 2\right)^{3} < 1$$
729 ---- < 1 1000
the solution of our inequality is:
$$x < -1$$
_____
\
-------ο-------
x1
Solving inequality on a graph

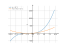 (x+2)^3
(x+2)^3
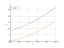 (x+2)^3
(x+2)^3