Mister Exam
Other calculators
- Square Inequality Step-by-Step
- Inequality with the module Step by Step
- Logarithmic inequality online
-
How to use it?
- Inequation:
- 7x<-3
- 1/2*(1/2)^2x-1-(1/2)^x-1>0
- (x^2-7*x-8)/(x^2-64)<0
- ((sqrt3)-2)(26-9x)<(sqrt3)/(2sqrt3+3)
- Derivative of:
-
tg3x
- 3/2
- Graphing y =:
- tg3x
- Integral of d{x}:
-
tg3x
-
3/2
- 3/2
-
Identical expressions
- tg three x>3/ two
- tg3x greater than 3 divide by 2
- tg three x greater than 3 divide by two
- tg3x>3 divide by 2
-
Similar expressions
- tg(3x)>-1
- cos(x/3+pi/7)˃=-(sqrt(3)/2)
- ((sqrt3)-2)(26-9x)<(sqrt3)/(2sqrt3+3)
- ctg(3x+pi/3)<√3
- ctg(3x)>1/3
tg3x>3/2 inequation
The solution
Detail solution
Given the inequality:
$$\tan{\left(3 x \right)} > \frac{3}{2}$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan{\left(3 x \right)} = \frac{3}{2}$$
Solve:
Given the equation
$$\tan{\left(3 x \right)} = \frac{3}{2}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$3 x = \pi n + \operatorname{atan}{\left(\frac{3}{2} \right)}$$
Or
$$3 x = \pi n + \operatorname{atan}{\left(\frac{3}{2} \right)}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
This roots
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$\left(\frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}\right) + - \frac{1}{10}$$
=
$$\frac{\pi n}{3} - \frac{1}{10} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
substitute to the expression
$$\tan{\left(3 x \right)} > \frac{3}{2}$$
$$\tan{\left(3 \left(\frac{\pi n}{3} - \frac{1}{10} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}\right) \right)} > \frac{3}{2}$$
Then
$$x < \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
no execute
the solution of our inequality is:
$$x > \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
$$\tan{\left(3 x \right)} > \frac{3}{2}$$
To solve this inequality, we must first solve the corresponding equation:
$$\tan{\left(3 x \right)} = \frac{3}{2}$$
Solve:
Given the equation
$$\tan{\left(3 x \right)} = \frac{3}{2}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$3 x = \pi n + \operatorname{atan}{\left(\frac{3}{2} \right)}$$
Or
$$3 x = \pi n + \operatorname{atan}{\left(\frac{3}{2} \right)}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
This roots
$$x_{1} = \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
$$x_{0} < x_{1}$$
For example, let's take the point
$$x_{0} = x_{1} - \frac{1}{10}$$
=
$$\left(\frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}\right) + - \frac{1}{10}$$
=
$$\frac{\pi n}{3} - \frac{1}{10} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
substitute to the expression
$$\tan{\left(3 x \right)} > \frac{3}{2}$$
$$\tan{\left(3 \left(\frac{\pi n}{3} - \frac{1}{10} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}\right) \right)} > \frac{3}{2}$$
tan(-3/10 + pi*n + atan(3/2)) > 3/2
Then
$$x < \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
no execute
the solution of our inequality is:
$$x > \frac{\pi n}{3} + \frac{\operatorname{atan}{\left(\frac{3}{2} \right)}}{3}$$
_____
/
-------ο-------
x1
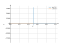
Solving inequality on a graph
Rapid solution
[src]
/ / / / atan(12/5) pi\\ \ \ | | |sin|- ---------- + --|| / ___________________________________________________\| | | pi | | \ 6 6 /| | / 2/ atan(12/5) pi\ 2/ atan(12/5) pi\ || | And|x < --, -I*|I*atan|----------------------| + log| / cos |- ---------- + --| + sin |- ---------- + --| || < x| | 6 | | / atan(12/5) pi\| \\/ \ 6 6 / \ 6 6 / /| | | | |cos|- ---------- + --|| | | \ \ \ \ 6 6 // / /
$$x < \frac{\pi}{6} \wedge - i \left(\log{\left(\sqrt{\sin^{2}{\left(- \frac{\operatorname{atan}{\left(\frac{12}{5} \right)}}{6} + \frac{\pi}{6} \right)} + \cos^{2}{\left(- \frac{\operatorname{atan}{\left(\frac{12}{5} \right)}}{6} + \frac{\pi}{6} \right)}} \right)} + i \operatorname{atan}{\left(\frac{\sin{\left(- \frac{\operatorname{atan}{\left(\frac{12}{5} \right)}}{6} + \frac{\pi}{6} \right)}}{\cos{\left(- \frac{\operatorname{atan}{\left(\frac{12}{5} \right)}}{6} + \frac{\pi}{6} \right)}} \right)}\right) < x$$
(x < pi/6)∧(-i*(i*atan(sin(-atan(12/5)/6 + pi/6)/cos(-atan(12/5)/6 + pi/6)) + log(sqrt(cos(-atan(12/5)/6 + pi/6)^2 + sin(-atan(12/5)/6 + pi/6)^2))) < x)