sin7x>sqrt(3/2) inequation

The solution

You have entered [src]

             _____
sin(7*x) > \/ 3/2

\sin{\left(7 x \right)} > \sqrt{\frac{3}{2}}

sin(7*x) > sqrt(3/2)

Detail solution

Given the inequality:

\sin{\left(7 x \right)} > \sqrt{\frac{3}{2}}

To solve this inequality, we must first solve the corresponding equation:

\sin{\left(7 x \right)} = \sqrt{\frac{3}{2}}

Solve:
Given the equation

\sin{\left(7 x \right)} = \sqrt{\frac{3}{2}}

- this is the simplest trigonometric equation
As right part of the equation
modulo =

True

but sin
can no be more than 1 or less than -1
so the solution of the equation d'not exist.

x_{1} = \frac{\pi}{7} - \frac{\operatorname{asin}{\left(\frac{\sqrt{6}}{2} \right)}}{7}

x_{2} = \frac{\operatorname{asin}{\left(\frac{\sqrt{6}}{2} \right)}}{7}

Exclude the complex solutions:
This equation has no roots,
this inequality is executed for any x value or has no solutions
check it
subtitute random point x, for example

x0 = 0

\sin{\left(0 \cdot 7 \right)} > \sqrt{\frac{3}{2}}

      ___
    \/ 6 
0 > -----
      2

so the inequality has no solutions

Solving inequality on a graph

Other calculators

How to use it?

Identical expressions

Similar expressions

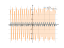sin7x>sqrt(3/2) inequation

The solution