Mister Exam

Other calculators

cosx=>0,5
Solving inequalities/ cosx=>0,5

cosx=>0,5 inequation

A inequation with variable

The solution

You have entered [src] 
cos(x) >= 1/2
cos⁡(x)≥12\cos{\left(x \right)} \geq \frac{1}{2} 
cos(x) >= 1/2
Detail solution
Given the inequality:
cos⁡(x)≥12\cos{\left(x \right)} \geq \frac{1}{2}
To solve this inequality, we must first solve the corresponding equation:
cos⁡(x)=12\cos{\left(x \right)} = \frac{1}{2}
Solve:
Given the equation
cos⁡(x)=12\cos{\left(x \right)} = \frac{1}{2}
- this is the simplest trigonometric equation
This equation is transformed to
x=2πn+acos⁡(12)x = 2 \pi n + \operatorname{acos}{\left(\frac{1}{2} \right)}
x=2πn−π+acos⁡(12)x = 2 \pi n - \pi + \operatorname{acos}{\left(\frac{1}{2} \right)}
Or
x=2πn+π3x = 2 \pi n + \frac{\pi}{3}
x=2πn−2π3x = 2 \pi n - \frac{2 \pi}{3}
, where n - is a integer
x1=2πn+π3x_{1} = 2 \pi n + \frac{\pi}{3}
x2=2πn−2π3x_{2} = 2 \pi n - \frac{2 \pi}{3}
x1=2πn+π3x_{1} = 2 \pi n + \frac{\pi}{3}
x2=2πn−2π3x_{2} = 2 \pi n - \frac{2 \pi}{3}
This roots
x1=2πn+π3x_{1} = 2 \pi n + \frac{\pi}{3}
x2=2πn−2π3x_{2} = 2 \pi n - \frac{2 \pi}{3}
is the points with change the sign of the inequality expression.
First define with the sign to the leftmost point:
x0≤x1x_{0} \leq x_{1}
For example, let's take the point
x0=x1−110x_{0} = x_{1} - \frac{1}{10}
=
(2πn+π3)−110\left(2 \pi n + \frac{\pi}{3}\right) - \frac{1}{10}
=
2πn−110+π32 \pi n - \frac{1}{10} + \frac{\pi}{3}
substitute to the expression
cos⁡(x)≥12\cos{\left(x \right)} \geq \frac{1}{2}
cos⁡(2πn−110+π3)≥12\cos{\left(2 \pi n - \frac{1}{10} + \frac{\pi}{3} \right)} \geq \frac{1}{2}
   /1    pi\       
sin|-- + --| >= 1/2
   \10   6 /

one of the solutions of our inequality is:
x≤2πn+π3x \leq 2 \pi n + \frac{\pi}{3}
 _____           _____          
      \         /
-------•-------•-------
       x_1      x_2

Other solutions will get with the changeover to the next point
etc.
The answer:
x≤2πn+π3x \leq 2 \pi n + \frac{\pi}{3}
x≥2πn−2π3x \geq 2 \pi n - \frac{2 \pi}{3}
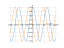
Solving inequality on a graph
05-20-15-10-51015202-2
Rapid solution 2 [src] 
    pi     5*pi       
[0, --] U [----, 2*pi)
    3       3
x in [0,π3]∪[5π3,2π)x\ in\ \left[0, \frac{\pi}{3}\right] \cup \left[\frac{5 \pi}{3}, 2 \pi\right) 
x in Union(Interval(0, pi/3), Interval.Ropen(5*pi/3, 2*pi))
Rapid solution [src] 
  /   /             pi\     /5*pi               \\
Or|And|0 <= x, x <= --|, And|---- <= x, x < 2*pi||
  \   \             3 /     \ 3                 //
(0≤x∧x≤π3)∨(5π3≤x∧x<2π)\left(0 \leq x \wedge x \leq \frac{\pi}{3}\right) \vee \left(\frac{5 \pi}{3} \leq x \wedge x < 2 \pi\right) 
((0 <= x)∧(x <= pi/3))∨((5*pi/3 <= x)∧(x < 2*pi))
The graph
cosx=>0,5 inequation
    © Mister Exam – Calculator