Mister Exam

Other calculators

Plotting a function graph/ tan(5*x)

Graphing y = tan(5*x)

v

The graph:

from to

Intersection points:

does show?

Piecewise:

The solution

You have entered [src] 
f(x) = tan(5*x)
f(x)=tan⁡(5x)f{\left(x \right)} = \tan{\left(5 x \right)} 
f = tan(5*x)
The graph of the function
02468-8-6-4-2-1010-5050
The points of intersection with the X-axis coordinate
Graph of the function intersects the axis X at f = 0
so we need to solve the equation:
tan⁡(5x)=0\tan{\left(5 x \right)} = 0
Solve this equation
The points of intersection with the axis X:

Analytical solution
x1=0x_{1} = 0
Numerical solution
x1=65.9734457253857x_{1} = 65.9734457253857
x2=−13.8230076757951x_{2} = -13.8230076757951
x3=26.3893782901543x_{3} = 26.3893782901543
x4=−21.9911485751286x_{4} = -21.9911485751286
x5=21.9911485751286x_{5} = 21.9911485751286
x6=96.1327351998477x_{6} = 96.1327351998477
x7=42.0973415581032x_{7} = 42.0973415581032
x8=4.39822971502571x_{8} = 4.39822971502571
x9=−76.026542216873x_{9} = -76.026542216873
x10=−15.707963267949x_{10} = -15.707963267949
x11=33.9292006587698x_{11} = 33.9292006587698
x12=16.3362817986669x_{12} = 16.3362817986669
x13=48.3805268652828x_{13} = 48.3805268652828
x14=−74.1415866247191x_{14} = -74.1415866247191
x15=99.9026463841554x_{15} = 99.9026463841554
x16=−64.0884901332318x_{16} = -64.0884901332318
x17=−20.1061929829747x_{17} = -20.1061929829747
x18=6.28318530717959x_{18} = 6.28318530717959
x19=−61.5752160103599x_{19} = -61.5752160103599
x20=74.1415866247191x_{20} = 74.1415866247191
x21=−32.0442450666159x_{21} = -32.0442450666159
x22=−30.159289474462x_{22} = -30.159289474462
x23=−77.9114978090269x_{23} = -77.9114978090269
x24=−33.9292006587698x_{24} = -33.9292006587698
x25=86.0796387083603x_{25} = 86.0796387083603
x26=14.451326206513x_{26} = 14.451326206513
x27=18.2212373908208x_{27} = 18.2212373908208
x28=28.2743338823081x_{28} = 28.2743338823081
x29=−99.9026463841554x_{29} = -99.9026463841554
x30=−71.6283125018473x_{30} = -71.6283125018473
x31=8.16814089933346x_{31} = 8.16814089933346
x32=58.4336233567702x_{32} = 58.4336233567702
x33=89.8495498926681x_{33} = 89.8495498926681
x34=−10.0530964914873x_{34} = -10.0530964914873
x35=23.8761041672824x_{35} = 23.8761041672824
x36=11.9380520836412x_{36} = 11.9380520836412
x37=−39.5840674352314x_{37} = -39.5840674352314
x38=−57.8053048260522x_{38} = -57.8053048260522
x39=38.3274303737955x_{39} = 38.3274303737955
x40=55.9203492338983x_{40} = 55.9203492338983
x41=−5.65486677646163x_{41} = -5.65486677646163
x42=−49.6371639267187x_{42} = -49.6371639267187
x43=−27.6460153515902x_{43} = -27.6460153515902
x44=72.2566310325652x_{44} = 72.2566310325652
x45=92.3628240155399x_{45} = 92.3628240155399
x46=45.867252742411x_{46} = 45.867252742411
x47=−87.9645943005142x_{47} = -87.9645943005142
x48=−69.7433569096934x_{48} = -69.7433569096934
x49=−1.88495559215388x_{49} = -1.88495559215388
x50=−93.6194610769758x_{50} = -93.6194610769758
x51=−37.6991118430775x_{51} = -37.6991118430775
x52=−43.9822971502571x_{52} = -43.9822971502571
x53=40.2123859659494x_{53} = 40.2123859659494
x54=−55.9203492338983x_{54} = -55.9203492338983
x55=36.4424747816416x_{55} = 36.4424747816416
x56=98.0176907920015x_{56} = 98.0176907920015
x57=−47.7522083345649x_{57} = -47.7522083345649
x58=62.2035345410779x_{58} = 62.2035345410779
x59=−79.7964534011807x_{59} = -79.7964534011807
x60=−11.9380520836412x_{60} = -11.9380520836412
x61=−23.8761041672824x_{61} = -23.8761041672824
x62=20.1061929829747x_{62} = 20.1061929829747
x63=−45.867252742411x_{63} = -45.867252742411
x64=−52.1504380495906x_{64} = -52.1504380495906
x65=−25.7610597594363x_{65} = -25.7610597594363
x66=−17.5929188601028x_{66} = -17.5929188601028
x67=76.026542216873x_{67} = 76.026542216873
x68=−81.6814089933346x_{68} = -81.6814089933346
x69=64.0884901332318x_{69} = 64.0884901332318
x70=−3.76991118430775x_{70} = -3.76991118430775
x71=−65.9734457253857x_{71} = -65.9734457253857
x72=54.0353936417444x_{72} = 54.0353936417444
x73=0x_{73} = 0
x74=80.4247719318987x_{74} = 80.4247719318987
x75=−35.8141562509236x_{75} = -35.8141562509236
x76=−98.0176907920015x_{76} = -98.0176907920015
x77=1.88495559215388x_{77} = 1.88495559215388
x78=60.318578948924x_{78} = 60.318578948924
x79=−83.5663645854885x_{79} = -83.5663645854885
x80=43.9822971502571x_{80} = 43.9822971502571
x81=67.8584013175395x_{81} = 67.8584013175395
x82=−54.0353936417444x_{82} = -54.0353936417444
x83=84.1946831162065x_{83} = 84.1946831162065
x84=−86.0796387083603x_{84} = -86.0796387083603
x85=−42.0973415581032x_{85} = -42.0973415581032
x86=−67.8584013175395x_{86} = -67.8584013175395
x87=50.2654824574367x_{87} = 50.2654824574367
x88=94.2477796076938x_{88} = 94.2477796076938
x89=82.3097275240526x_{89} = 82.3097275240526
x90=−59.6902604182061x_{90} = -59.6902604182061
x91=52.1504380495906x_{91} = 52.1504380495906
x92=70.3716754404114x_{92} = 70.3716754404114
x93=−96.1327351998477x_{93} = -96.1327351998477
x94=−7.5398223686155x_{94} = -7.5398223686155
x95=10.0530964914873x_{95} = 10.0530964914873
x96=−89.8495498926681x_{96} = -89.8495498926681
x97=30.159289474462x_{97} = 30.159289474462
x98=87.9645943005142x_{98} = 87.9645943005142
x99=32.0442450666159x_{99} = 32.0442450666159
x100=77.9114978090269x_{100} = 77.9114978090269
x101=−91.734505484822x_{101} = -91.734505484822
The points of intersection with the Y axis coordinate
The graph crosses Y axis when x equals 0:
substitute x = 0 to tan(5*x).
tan⁡(0⋅5)\tan{\left(0 \cdot 5 \right)}
The result:
f(0)=0f{\left(0 \right)} = 0
The point:
(0, 0)
Extrema of the function
In order to find the extrema, we need to solve the equation
ddxf(x)=0\frac{d}{d x} f{\left(x \right)} = 0
(the derivative equals zero),
and the roots of this equation are the extrema of this function:
ddxf(x)=\frac{d}{d x} f{\left(x \right)} =
the first derivative
5tan⁡2(5x)+5=05 \tan^{2}{\left(5 x \right)} + 5 = 0
Solve this equation
Solutions are not found,
function may have no extrema
Inflection points
Let's find the inflection points, we'll need to solve the equation for this
d2dx2f(x)=0\frac{d^{2}}{d x^{2}} f{\left(x \right)} = 0
(the second derivative equals zero),
the roots of this equation will be the inflection points for the specified function graph:
d2dx2f(x)=\frac{d^{2}}{d x^{2}} f{\left(x \right)} =
the second derivative
50(tan⁡2(5x)+1)tan⁡(5x)=050 \left(\tan^{2}{\left(5 x \right)} + 1\right) \tan{\left(5 x \right)} = 0
Solve this equation
The roots of this equation
x1=0x_{1} = 0

Сonvexity and concavity intervals:
Let’s find the intervals where the function is convex or concave, for this look at the behaviour of the function at the inflection points:
Concave at the intervals
[0,∞)\left[0, \infty\right)
Convex at the intervals
(−∞,0]\left(-\infty, 0\right]
Horizontal asymptotes
Let’s find horizontal asymptotes with help of the limits of this function at x->+oo and x->-oo
lim⁡x→−∞tan⁡(5x)=⟨−∞,∞⟩\lim_{x \to -\infty} \tan{\left(5 x \right)} = \left\langle -\infty, \infty\right\rangle
Let's take the limit
so,
equation of the horizontal asymptote on the left:
y=⟨−∞,∞⟩y = \left\langle -\infty, \infty\right\rangle
lim⁡x→∞tan⁡(5x)=⟨−∞,∞⟩\lim_{x \to \infty} \tan{\left(5 x \right)} = \left\langle -\infty, \infty\right\rangle
Let's take the limit
so,
equation of the horizontal asymptote on the right:
y=⟨−∞,∞⟩y = \left\langle -\infty, \infty\right\rangle
Inclined asymptotes
Inclined asymptote can be found by calculating the limit of tan(5*x), divided by x at x->+oo and x ->-oo
True

Let's take the limit
so,
inclined asymptote equation on the left:
y=xlim⁡x→−∞(tan⁡(5x)x)y = x \lim_{x \to -\infty}\left(\frac{\tan{\left(5 x \right)}}{x}\right)
True

Let's take the limit
so,
inclined asymptote equation on the right:
y=xlim⁡x→∞(tan⁡(5x)x)y = x \lim_{x \to \infty}\left(\frac{\tan{\left(5 x \right)}}{x}\right)
Even and odd functions
Let's check, whether the function even or odd by using relations f = f(-x) и f = -f(-x).
So, check:
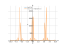tan⁡(5x)=−tan⁡(5x)\tan{\left(5 x \right)} = - \tan{\left(5 x \right)}
- No
tan⁡(5x)=tan⁡(5x)\tan{\left(5 x \right)} = \tan{\left(5 x \right)}
- Yes
so, the function
is
odd
    © Mister Exam – Calculator