Intégrale double étape par étape

Avec la bonne solution de l’intégrale, tu seras le plus apprécié du groupe ❤️😊

Fonctionnalités?

• Calcule l’intégrale double sur une région délimitée par les lignes indiquées (ici), en posant ainsi les bornes d’intégration ici
• Calcule, via l’intégrale double, l’aire d’une figure délimitée par des lignes
• Calcule des intégrales itérées (avec des bornes déjà connues)
• Écrit l’intégrale double de f(x, y) sous forme itérée
• Calcule la masse d’une plaque via l’intégrale double
• Permutation de l’ordre d’intégration dans l’intégrale itérée (ici)
• S’il est pertinent d’utiliser polaires coordonnées, alors elles sont utilisées

Calcul de l’aire

Pour calculer l’aire de la figure délimitée par des lignes à l’aide de l’intégrale double, remplacez l’intégrande simplement par 1. Il est également possible d’utiliser le calculateur suivant: Aire de la figure entre des courbes

Exemples d’intégrales doubles

Comment définir la région D?

La région D peut être définie de différentes manières:

• Par des lignes courbes:
  1. Cercle
  2. Deux cercles
  3. Ellipse
  4. Parabole
  5. Autres
• À l’aide de sommets:
  1. Triangle

     A(0, 1)

     B(1, 0)

     C(0, 0)

  2. Carré
  3. Rectangle
• et — quadrant

Sous forme d’inégalité

Définissez la contrainte pour la région d’intégration sous forme d’inégalité:

x > pi/2

-1/2 < y <= 3/2

x < sqrt(2)/2 + 1

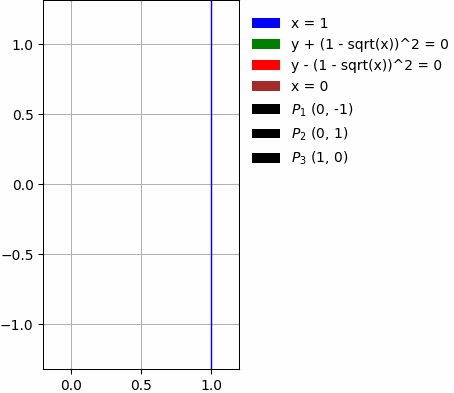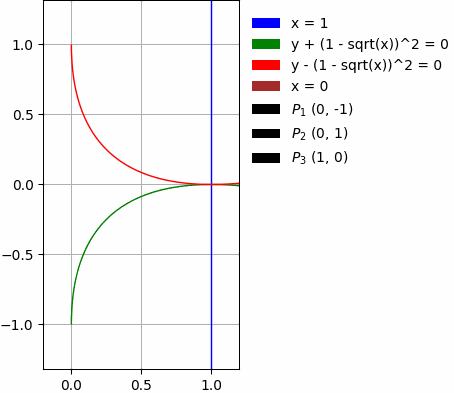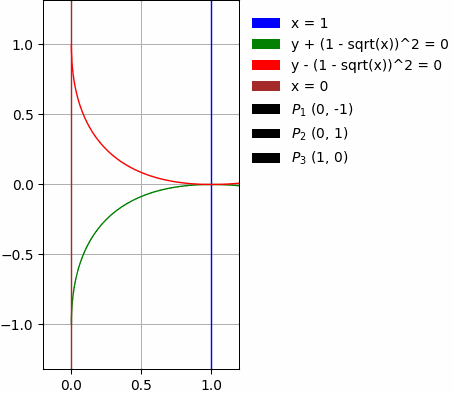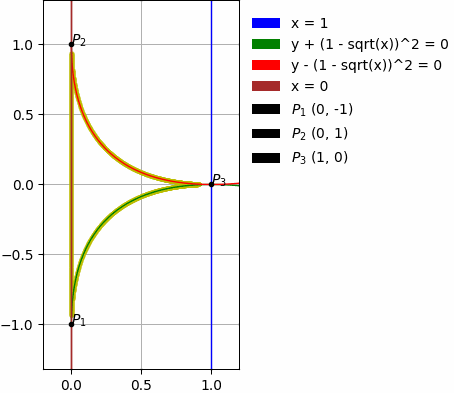
Les exemples ci-dessus contiennent aussi:

• valeur absolue ou valeur absolue: absolute(x) ou |x|
• racines carrées sqrt(x),
  racines cubiques cbrt(x)
• fonctions trigonométriques:
  sinus sin(x), cosinus cos(x), tangente tan(x), cotangente ctan(x)
• fonctions exponentielles et exposants exp(x)
• fonctions trigonométriques inverses:
  arcsinus asin(x), arccosinus acos(x), arctangente atan(x), arccotangente acot(x)
• logarithmes naturels ln(x),
  logarithmes décimaux log(x)
• fonctions hyperboliques:
  sinus hyperbolique sh(x), cosinus hyperbolique ch(x), tangente hyperbolique et cotangente hyperbolique tanh(x), ctanh(x)
• fonctions hyperboliques inverses:
  arcsinus hyperbolique asinh(x), arccosinus hyperbolique acosh(x), arctangente hyperbolique atanh(x), arccotangente hyperbolique acoth(x)
• autres fonctions trigonométriques et hyperboliques:
  sécante sec(x), cosécante csc(x), arcsecante asec(x), arccosécante acsc(x), sécante hyperbolique sech(x), cosécante hyperbolique csch(x), arcsecante hyperbolique asech(x), arccosécante hyperbolique acsch(x)
• fonctions d’arrondi:
  plancher floor(x), plafond ceiling(x)
• signe du nombre:
  sign(x)
• pour la théorie des probabilités:
  fonction d’erreur erf(x) (intégrale de probabilité), fonction de Laplace laplace(x)
• Factorielle de x:
  x! ou factorial(x)
• fonction Gamma gamma(x)
• fonction de Lambert W LambertW(x)
• intégrales trigonométriques: Si(x), Ci(x), Shi(x), Chi(x)

règles de saisie

Les opérations suivantes sont possibles

2*x

- multiplication

3/x

- division

x^2

- élévation au carré

x^3

- élévation au cube

x^5

- élévation à une puissance

x + 7

- addition

x - 6

- soustraction

Nombres réels

saisir sous la forme 7.5, pas 7,5

Constantes

pi

- nombre pi

e

- base du logarithme naturel

i

- nombre complexe

oo

- symbole de l’infini

Ces exemples peuvent également être utilisés pour saisir les bornes supérieure et inférieure dans une intégrale double.