Mister Exam

Other calculators

x^2-5x+9=0

x^2-5x+9=0 equation

The teacher will be very surprised to see your correct solution 😉

v

Numerical solution:

Do search numerical solution at [, ]

The solution

You have entered [src] 
 2              
x  - 5*x + 9 = 0
x2−5x+9=0x^{2} - 5 x + 9 = 0
Simplify
Detail solution
This equation is of the form
a∗x2+b∗x+c=0a*x^2 + b*x + c = 0
A quadratic equation can be solved using the discriminant
The roots of the quadratic equation:
x1=D−b2ax_{1} = \frac{\sqrt{D} - b}{2 a}
x2=−D−b2ax_{2} = \frac{- \sqrt{D} - b}{2 a}
where D=b2−4acD = b^2 - 4 a c is the discriminant.
Because
a=1a = 1
b=−5b = -5
c=9c = 9
, then
D=b2−4∗a∗c=D = b^2 - 4 * a * c =
(−1)1⋅4⋅9+(−5)2=−11\left(-1\right) 1 \cdot 4 \cdot 9 + \left(-5\right)^{2} = -11
Because D<0, then the equation
has no real roots,
but complex roots is exists.
x1=(−b+D)2ax_1 = \frac{(-b + \sqrt{D})}{2 a}
x2=(−b−D)2ax_2 = \frac{(-b - \sqrt{D})}{2 a}
or
x1=52+11i2x_{1} = \frac{5}{2} + \frac{\sqrt{11} i}{2}
Simplify
x2=52−11i2x_{2} = \frac{5}{2} - \frac{\sqrt{11} i}{2}
Simplify
Vieta's Theorem
it is reduced quadratic equation
px+x2+q=0p x + x^{2} + q = 0
where
p=bap = \frac{b}{a}
p=−5p = -5
q=caq = \frac{c}{a}
q=9q = 9
Vieta Formulas
x1+x2=−px_{1} + x_{2} = - p
x1x2=qx_{1} x_{2} = q
x1+x2=5x_{1} + x_{2} = 5
x1x2=9x_{1} x_{2} = 9
The graph
0123456789-2-1020
Plot the graph f1(x)
Plot the graph f2(x)
Rapid solution [src] 
              ____
      5   I*\/ 11 
x_1 = - - --------
      2      2
x1=52−11i2x_{1} = \frac{5}{2} - \frac{\sqrt{11} i}{2}
Simplify 
              ____
      5   I*\/ 11 
x_2 = - + --------
      2      2
x2=52+11i2x_{2} = \frac{5}{2} + \frac{\sqrt{11} i}{2}
Simplify
Sum and product of roots [src] 
sum
        ____           ____
5   I*\/ 11    5   I*\/ 11 
- - -------- + - + --------
2      2       2      2
(52−11i2)+(52+11i2)\left(\frac{5}{2} - \frac{\sqrt{11} i}{2}\right) + \left(\frac{5}{2} + \frac{\sqrt{11} i}{2}\right) 
=
5
55
Simplify 
product
        ____           ____
5   I*\/ 11    5   I*\/ 11 
- - -------- * - + --------
2      2       2      2
(52−11i2)∗(52+11i2)\left(\frac{5}{2} - \frac{\sqrt{11} i}{2}\right) * \left(\frac{5}{2} + \frac{\sqrt{11} i}{2}\right) 
=
9
99
Simplify
Numerical answer [src] 
x1 = 2.5 + 1.6583123951777*i
x2 = 2.5 - 1.6583123951777*i
x2 = 2.5 - 1.6583123951777*i
The graph
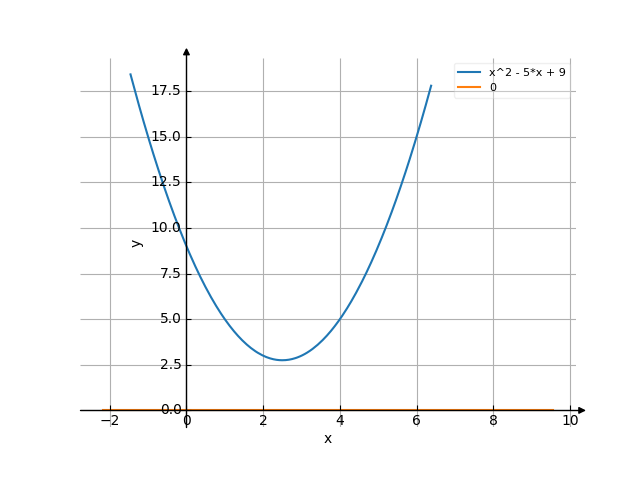
x^2-5x+9=0 equation
    © Mister Exam – Calculator