Mister Exam
Other calculators
-
How to use it?
- Equation:
- Equation (x2+y2–1)3-x2y3=0
-
Equation tgx=1
- Equation (x+7)^4+(x+7)^2-30=0
-
Equation (x-5)(x-1)-21=0
- Express {x} in terms of y where:
- 60x^2y+75x^2y^2+120xy^260x2y+75x2y2+120xy2приx=-0,5x=−0,5,y=0,4y=0,4.
- (x-17)^2+(y+26)^2=16(x−17)2+(y+26)2=16.
- 5*x-5*y=20
- 8*x-7*y=-13
-
Identical expressions
- (x2+y2– one) three -x2y3= zero
- (x2 plus y2–1)3 minus x2y3 equally 0
- (x2 plus y2– one) three minus x2y3 equally zero
- x2+y2–13-x2y3=0
- (x2+y2–1)3-x2y3=O
-
Similar expressions
- (x2+y2–1)3+x2y3=0
- (x2-y2–1)3-x2y3=0
-
What you mean?
- -x^2*y^3 + (x^2 + y^2 - 1*1)^3 = 0
You entered:
(x2+y2–1)3-x2y3=0
What you mean?
(x2+y2–1)3-x2y3=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution set is obviously symmetric with respect to the $y$-axis. Therefore we may assume $x\geq 0$. In the domain $\{(x,y)\in {\mathbb R}^2\ |\ x\geq0\}$ the equation is equivalent with\n$$x^2+ y^2 -1=x^{2/3} y\ ,$$\nwhich can easily be solved for $y$:\n$$y={1\over2}\bigl(x^{2/3}\pm\sqrt{x^{4/3}+4(1-x^2)}\bigr)\ .$$\nNow plot this, taking both branches of the square root into account. You might have to numerically solve the equation $x^{4/3}+4(1-x^2)=0$ in order to get the exact $x$-interval.
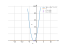
The solution
You have entered
[src]
(x2 + y2 - 1)*3 - x2*y3 = 0
$$- x_{2} y_{3} + \left(x_{2} + y_{2} - 1\right) 3 = 0$$
Detail solution
Given the linear equation:
Expand brackets in the left part
Looking for similar summands in the left part:
Move free summands (without y3)
from left part to right part, we given:
$$- x_{2} y_{3} + 3 x_{2} + 3 y_{2} = 3$$
Move the summands with the other variables
from left part to right part, we given:
$$- x_{2} y_{3} + 3 y_{2} = - 3 x_{2} + 3$$
Divide both parts of the equation by (3*y2 - x2*y3)/y3
We get the answer: y3 = 3*(-1 + x2 + y2)/x2
(x2+y2-1)*3-x2*y3 = 0
Expand brackets in the left part
x2*3+y2*3-1*3-x2*y3 = 0
Looking for similar summands in the left part:
-3 + 3*x2 + 3*y2 - x2*y3 = 0
Move free summands (without y3)
from left part to right part, we given:
$$- x_{2} y_{3} + 3 x_{2} + 3 y_{2} = 3$$
Move the summands with the other variables
from left part to right part, we given:
$$- x_{2} y_{3} + 3 y_{2} = - 3 x_{2} + 3$$
Divide both parts of the equation by (3*y2 - x2*y3)/y3
y3 = 3 - 3*x2 / ((3*y2 - x2*y3)/y3)
We get the answer: y3 = 3*(-1 + x2 + y2)/x2
The solution of the parametric equation
Given the equation with a parameter:
$$- x_{2} y_{3} + 3 x_{2} + 3 y_{2} - 3 = 0$$
The coefficient at y3 is equal to
$$- x_{2}$$
then possible cases for x2 :
$$x_{2} < 0$$
$$x_{2} = 0$$
Consider all cases in more detail:
With
$$x_{2} < 0$$
the equation
$$3 y_{2} + y_{3} - 6 = 0$$
its solution
$$y_{3} = - 3 y_{2} + 6$$
With
$$x_{2} = 0$$
the equation
$$3 y_{2} - 3 = 0$$
its solution
$$- x_{2} y_{3} + 3 x_{2} + 3 y_{2} - 3 = 0$$
The coefficient at y3 is equal to
$$- x_{2}$$
then possible cases for x2 :
$$x_{2} < 0$$
$$x_{2} = 0$$
Consider all cases in more detail:
With
$$x_{2} < 0$$
the equation
$$3 y_{2} + y_{3} - 6 = 0$$
its solution
$$y_{3} = - 3 y_{2} + 6$$
With
$$x_{2} = 0$$
the equation
$$3 y_{2} - 3 = 0$$
its solution
The graph
Rapid solution
[src]
3*(-1 + x2 + y2)
y3_1 = ----------------
x2
$$y_{3 1} = \frac{3 \left(x_{2} + y_{2} - 1\right)}{x_{2}}$$
Sum and product of roots
[src]
sum
3*(-1 + x2 + y2)
----------------
x2
$$\left(\frac{3 \left(x_{2} + y_{2} - 1\right)}{x_{2}}\right)$$
=
3*(-1 + x2 + y2)
----------------
x2
$$\frac{3 \left(x_{2} + y_{2} - 1\right)}{x_{2}}$$
product
3*(-1 + x2 + y2)
----------------
x2
$$\left(\frac{3 \left(x_{2} + y_{2} - 1\right)}{x_{2}}\right)$$
=
3*(-1 + x2 + y2)
----------------
x2
$$\frac{3 \left(x_{2} + y_{2} - 1\right)}{x_{2}}$$