Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation sin(6x)-cos(3x)=0
-
Equation ctg²5x-ctg5x=0
- Equation (d+7)(-d-7)+(2d-1)
- Equation sin^3x+cos^3x=sin^2x+cos^2x
- Express {x} in terms of y where:
- -1*x-19*y=-10
- 4*x-16*y=6
- 5*x+5*y=20
- 10*x-1*y=10
-
Identical expressions
- sin(6x)-cos(3x)= zero
- sinus of (6x) minus co sinus of e of (3x) equally 0
- sinus of (6x) minus co sinus of e of (3x) equally zero
- sin6x-cos3x=0
- sin(6x)-cos(3x)=O
-
Similar expressions
- sin(6x)+cos(3x)=0
sin(6x)-cos(3x)=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
You have entered
[src]
sin(6*x) - cos(3*x) = 0
$$\sin{\left(6 x \right)} - \cos{\left(3 x \right)} = 0$$
Detail solution
Given the equation:
$$\sin{\left(6 x \right)} - \cos{\left(3 x \right)} = 0$$
Transform
$$\sin{\left(6 x \right)} - \cos{\left(3 x \right)} = 0$$
$$\left(2 \sin{\left(3 x \right)} - 1\right) \cos{\left(3 x \right)} = 0$$
Consider each factor separately
$$2 \sin{\left(3 x \right)} - 1 = 0$$
- this is the simplest trigonometric equation
Move $-1$ to right part of the equation
with the change of sign in $-1$
We get:
$$2 \sin{\left(3 x \right)} = 1$$
Divide both parts of the equation by $2$
The equation is transformed to
$$\sin{\left(3 x \right)} = \frac{1}{2}$$
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{asin}{\left(\frac{1}{2} \right)}$$
$$3 x = 2 \pi n - \operatorname{asin}{\left(\frac{1}{2} \right)} + \pi$$
Or
$$3 x = 2 \pi n + \frac{\pi}{6}$$
$$3 x = 2 \pi n + \frac{5 \pi}{6}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
get the intermediate answer:
$$x = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
$$\cos{\left(3 x \right)} = 0$$
- this is the simplest trigonometric equation
We get:
$$\cos{\left(3 x \right)} = 0$$
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{acos}{\left(0 \right)}$$
$$3 x = 2 \pi n - \pi + \operatorname{acos}{\left(0 \right)}$$
Or
$$3 x = 2 \pi n + \frac{\pi}{2}$$
$$3 x = 2 \pi n - \frac{\pi}{2}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
get the intermediate answer:
$$x = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{\pi}{6}$$
$$x = \frac{2 \pi n}{3} - \frac{\pi}{6}$$
The final answer:
$$x_{1} = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x_{2} = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
$$x_{3} = \frac{2 \pi n}{3} + \frac{\pi}{6}$$
$$x_{4} = \frac{2 \pi n}{3} - \frac{\pi}{6}$$
$$\sin{\left(6 x \right)} - \cos{\left(3 x \right)} = 0$$
Transform
$$\sin{\left(6 x \right)} - \cos{\left(3 x \right)} = 0$$
$$\left(2 \sin{\left(3 x \right)} - 1\right) \cos{\left(3 x \right)} = 0$$
Consider each factor separately
Step
$$2 \sin{\left(3 x \right)} - 1 = 0$$
- this is the simplest trigonometric equation
Move $-1$ to right part of the equation
with the change of sign in $-1$
We get:
$$2 \sin{\left(3 x \right)} = 1$$
Divide both parts of the equation by $2$
The equation is transformed to
$$\sin{\left(3 x \right)} = \frac{1}{2}$$
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{asin}{\left(\frac{1}{2} \right)}$$
$$3 x = 2 \pi n - \operatorname{asin}{\left(\frac{1}{2} \right)} + \pi$$
Or
$$3 x = 2 \pi n + \frac{\pi}{6}$$
$$3 x = 2 \pi n + \frac{5 \pi}{6}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
get the intermediate answer:
$$x = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
Step
$$\cos{\left(3 x \right)} = 0$$
- this is the simplest trigonometric equation
We get:
$$\cos{\left(3 x \right)} = 0$$
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{acos}{\left(0 \right)}$$
$$3 x = 2 \pi n - \pi + \operatorname{acos}{\left(0 \right)}$$
Or
$$3 x = 2 \pi n + \frac{\pi}{2}$$
$$3 x = 2 \pi n - \frac{\pi}{2}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
get the intermediate answer:
$$x = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
$$x = \frac{2 \pi n}{3} + \frac{\pi}{6}$$
$$x = \frac{2 \pi n}{3} - \frac{\pi}{6}$$
The final answer:
$$x_{1} = \frac{2 \pi n}{3} + \frac{\pi}{18}$$
$$x_{2} = \frac{2 \pi n}{3} + \frac{5 \pi}{18}$$
$$x_{3} = \frac{2 \pi n}{3} + \frac{\pi}{6}$$
$$x_{4} = \frac{2 \pi n}{3} - \frac{\pi}{6}$$
Sum and product of roots
[src]
sum
-5*pi -pi -pi pi pi 5*pi ----- + ---- + ---- + -- + -- + ---- 6 2 6 6 2 6
$$\left(- \frac{5 \pi}{6}\right) + \left(- \frac{\pi}{2}\right) + \left(- \frac{\pi}{6}\right) + \left(\frac{\pi}{6}\right) + \left(\frac{\pi}{2}\right) + \left(\frac{5 \pi}{6}\right)$$
=
0
$$0$$
product
-5*pi -pi -pi pi pi 5*pi ----- * ---- * ---- * -- * -- * ---- 6 2 6 6 2 6
$$\left(- \frac{5 \pi}{6}\right) * \left(- \frac{\pi}{2}\right) * \left(- \frac{\pi}{6}\right) * \left(\frac{\pi}{6}\right) * \left(\frac{\pi}{2}\right) * \left(\frac{5 \pi}{6}\right)$$
=
6 -25*pi ------- 5184
$$- \frac{25 \pi^{6}}{5184}$$
Rapid solution
[src]
-5*pi
x_1 = -----
6
$$x_{1} = - \frac{5 \pi}{6}$$
-pi
x_2 = ----
2
$$x_{2} = - \frac{\pi}{2}$$
-pi
x_3 = ----
6
$$x_{3} = - \frac{\pi}{6}$$
pi
x_4 = --
6
$$x_{4} = \frac{\pi}{6}$$
pi
x_5 = --
2
$$x_{5} = \frac{\pi}{2}$$
5*pi
x_6 = ----
6
$$x_{6} = \frac{5 \pi}{6}$$
Numerical answer
[src]
x1 = 26.0054058547155
x2 = 39.9680398706701
x3 = -91.9788515801012
x4 = -20.0712863979348
x5 = 7.15584993317675
x6 = -71.733032256967
x7 = 38.2227106186758
x8 = 4.36332312998582
x9 = 30.1941960595019
x10 = 92.3279174305
x11 = 56.025068989018
x12 = 53.9306738866248
x13 = -39.6189740202713
x14 = 67.8933079025794
x15 = -4.01425727958696
x16 = 83.9503370209273
x17 = -85.6956662729216
x18 = 60.2138591938044
x19 = 2.26892802759263
x20 = -5.75958653158129
x21 = -25.6563400043166
x22 = -61.9591884457987
x23 = -43.8077642250577
x24 = -29.845130209103
x25 = -79.412480965742
x26 = 80.1106126665397
x27 = -53.9306738866248
x28 = 18.3259571459405
x29 = -73.8274273593601
x30 = 55.3269372882203
x31 = 46.2512251778497
x32 = -31.9395253114962
x33 = 178.54718247902
x34 = -7.85398163397448
x35 = 86.0447321233204
x36 = -100.007366139275
x37 = -45.9021593274509
x38 = 65.1007810993885
x39 = 62.3082542961976
x40 = -13.7881010907552
x41 = -37.1755130674792
x42 = 48.3456202802429
x43 = -22.165681500328
x44 = 12.0427718387609
x45 = 16.2315620435473
x46 = -59.8647933434055
x47 = -41.7133691226645
x48 = -12.3918376891597
x49 = 6.80678408277789
x50 = -49.7418836818384
x51 = 14.1371669411541
x52 = 94.4223125328932
x53 = 44.1568300754565
x54 = 0.174532925199433
x55 = 28.0998009571087
x56 = 100.007366139275
x57 = -36.1283155162826
x58 = -4.71238898038469
x59 = 78.0162175641465
x60 = -95.8185759344887
x61 = -87.7900613753148
x62 = -93.7241808320955
x63 = -34.0339204138894
x64 = 97.9129710368819
x65 = 36.1283155162826
x66 = -66.1479786505851
x67 = -51.8362787842316
x68 = -78.0162175641465
x69 = 72.0820981073658
x70 = -80.1106126665397
x71 = 74.176493209759
x72 = -75.9218224617533
x73 = 34.0339204138894
x74 = -97.9129710368819
x75 = -15.8824961931484
x76 = -83.6012711705284
x77 = -56.025068989018
x78 = 90.2335223281068
x79 = 88.1391272257137
x80 = 50.789081233035
x81 = -47.9965544298441
x82 = -27.7507351067098
x83 = -64.0535835481919
x84 = 42.0624349730633
x85 = -1.91986217719376
x86 = -89.884456477708
x87 = -9.94837673636768
x88 = 82.2050077689329
x89 = -17.9768912955416
x90 = -69.6386371545737
x91 = 58.1194640914112
x92 = 69.9877030049726
x93 = -70.3367688553715
x94 = 2.61799387799149
x95 = -57.7703982410123
x96 = 23.9110107523223
x97 = 65.4498469497874
x98 = 76.2708883121522
x99 = 641.059434257517
x100 = 9.94837673636768
x100 = 9.94837673636768
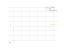
The graph