Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation ctg(x/2)=√3
- Equation (y^3+4y^2-6)-(5y-y^3+6)=2y^3+4y^2+y
- Equation ((x+6)/(x+5))+((10)/((x^2)-25))=5/4
-
Equation sin(3x)=-sqrt3/2
- Express {x} in terms of y where:
- 15*x+15*y=16
- -4*x+18*y=-14
- 8*x+7*y=-13
- 14*x-16*y=14
- Graphing y =:
-
sin(3x)
- Canonical form:
- sin(3x)
- Integral of d{x}:
-
sin(3x)
-
Identical expressions
- sin(3x)=-sqrt3/ two
- sinus of (3x) equally minus square root of 3 divide by 2
- sinus of (3x) equally minus square root of 3 divide by two
- sin(3x)=-√3/2
- sin3x=-sqrt3/2
- sin(3x)=-sqrt3 divide by 2
-
Similar expressions
- sin2x=-(sqrt3/2)
- sin^3x+cos^3x=sin^2x+cos^2x
- sin(3x-1)-1=-0,5
- sin(x)+sqrt(((2-sqrt(3))/2)(cos(x)+1))=0
- Cos3xcos5x-sin3xsin5x=0
- sin(3x)=+sqrt3/2
- sin(5x/2)*sin(3x/2)+cos(5x/2)*cos(3x/2)=0
sin(3x)=-sqrt3/2 equation
The teacher will be very surprised to see your correct solution 😉
The solution
You have entered
[src]
___
-\/ 3
sin(3*x) = -------
2
$$\sin{\left(3 x \right)} = \frac{\left(-1\right) \sqrt{3}}{2}$$
Detail solution
Given the equation
$$\sin{\left(3 x \right)} = \frac{\left(-1\right) \sqrt{3}}{2}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{asin}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$3 x = 2 \pi n - \operatorname{asin}{\left(- \frac{\sqrt{3}}{2} \right)} + \pi$$
Or
$$3 x = 2 \pi n - \frac{\pi}{3}$$
$$3 x = 2 \pi n + \frac{4 \pi}{3}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
we get the answer:
$$x_{1} = \frac{2 \pi n}{3} - \frac{\pi}{9}$$
$$x_{2} = \frac{2 \pi n}{3} + \frac{4 \pi}{9}$$
$$\sin{\left(3 x \right)} = \frac{\left(-1\right) \sqrt{3}}{2}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$3 x = 2 \pi n + \operatorname{asin}{\left(- \frac{\sqrt{3}}{2} \right)}$$
$$3 x = 2 \pi n - \operatorname{asin}{\left(- \frac{\sqrt{3}}{2} \right)} + \pi$$
Or
$$3 x = 2 \pi n - \frac{\pi}{3}$$
$$3 x = 2 \pi n + \frac{4 \pi}{3}$$
, where n - is a integer
Divide both parts of the equation by
$$3$$
we get the answer:
$$x_{1} = \frac{2 \pi n}{3} - \frac{\pi}{9}$$
$$x_{2} = \frac{2 \pi n}{3} + \frac{4 \pi}{9}$$
Sum and product of roots
[src]
sum
pi 4*pi
0 - -- + ----
9 9
$$\left(- \frac{\pi}{9} + 0\right) + \frac{4 \pi}{9}$$
=
pi -- 3
$$\frac{\pi}{3}$$
product
-pi 4*pi 1*----*---- 9 9
$$\frac{4 \pi}{9} \cdot 1 \left(- \frac{\pi}{9}\right)$$
=
2 -4*pi ------ 81
$$- \frac{4 \pi^{2}}{81}$$
-4*pi^2/81
Rapid solution
[src]
-pi
x1 = ----
9
$$x_{1} = - \frac{\pi}{9}$$
4*pi
x2 = ----
9
$$x_{2} = \frac{4 \pi}{9}$$
Numerical answer
[src]
x1 = -49469.9613843777
x2 = -90.4080552533063
x3 = -84.1248699461267
x4 = 3.83972435438753
x5 = 45.7276264022514
x6 = -15.3588974175501
x7 = 56.1996019142174
x8 = 70.5113017805709
x9 = -63.5299847725936
x10 = -0.349065850398866
x11 = 5.93411945678072
x12 = 43.6332312998582
x13 = 20.2458193231342
x14 = -61.4355896702004
x15 = 33.1612557878923
x16 = -75.7472895365539
x17 = -44.331363000656
x18 = -46.4257581030492
x19 = -65.6243798749868
x20 = -10.8210413623648
x21 = 98.0875039620813
x22 = -42.2369678982628
x23 = 87.6155284501153
x24 = 93.8987137572949
x25 = -19.5476876223365
x26 = -88.3136601509131
x27 = 30.7177948351002
x28 = -67.71877497738
x29 = -77.8416846389471
x30 = -69.8131700797732
x31 = 100.181899064475
x32 = -21.2930168743308
x33 = -23.7364778271229
x34 = 68.4169066781777
x35 = 74.7000919853573
x36 = 83.0776723949301
x37 = -27.9252680319093
x38 = -59.3411945678072
x39 = -56.8977336150151
x40 = 64.2281164733913
x41 = 24.4346095279206
x42 = 14.3116998663535
x43 = -74.0019602845596
x44 = 8.02851455917392
x45 = -54.8033385126219
x46 = -31.7649923862968
x47 = 52.010811709431
x48 = 60.0393262686049
x49 = 1.74532925199433
x50 = 72.6056968829641
x51 = -21.6420827247297
x52 = -25.8308729295161
x53 = -38.0481776934764
x54 = 10.1229096615671
x55 = -76.0963553869528
x56 = -2.44346095279206
x57 = 62.1337213709981
x58 = -86.2192650485199
x59 = 66.6715774261834
x60 = 18.151424220741
x61 = -6.63225115757845
x62 = 91.8043186549017
x63 = -92.5024503556995
x64 = -46.774823953448
x65 = 16.0570291183478
x66 = 85.5211333477222
x67 = 77.1435529381494
x68 = -13.2645023151569
x69 = -33.85938748869
x70 = -79.9360797413403
x71 = 54.1052068118242
x72 = -57.246799465414
x73 = -17.4532925199433
x74 = -35.9537825910832
x75 = -30.0196631343025
x76 = -94.9459113084915
x77 = 49.9164166070378
x78 = 89.7099235525085
x79 = 12.2173047639603
x80 = 39.095375244673
x81 = -82.0304748437335
x82 = -71.9075651821664
x83 = -4.88692190558412
x84 = 47.8220215046446
x85 = -50.6145483078356
x86 = -19.1986217719376
x87 = 26.5290046303138
x88 = 66.3225115757845
x89 = 22.3402144255274
x90 = 41.538836197465
x91 = 58.2939970166106
x92 = 28.623399732707
x93 = -40.1425727958696
x94 = 95.9931088596881
x95 = -126.361837844389
x96 = -469.493568786475
x96 = -469.493568786475
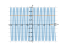
The graph