k^2-4*k+13=0 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
This equation is of the form
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$k_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$k_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = -4$$
$$c = 13$$
, then
Because D<0, then the equation
has no real roots,
but complex roots is exists.
or
$$k_{1} = 2 + 3 i$$
Simplify
$$k_{2} = 2 - 3 i$$
Simplify
a*k^2 + b*k + c = 0
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$k_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$k_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = -4$$
$$c = 13$$
, then
D = b^2 - 4 * a * c =
(-4)^2 - 4 * (1) * (13) = -36
Because D<0, then the equation
has no real roots,
but complex roots is exists.
k1 = (-b + sqrt(D)) / (2*a)
k2 = (-b - sqrt(D)) / (2*a)
or
$$k_{1} = 2 + 3 i$$
Simplify
$$k_{2} = 2 - 3 i$$
Simplify
Vieta's Theorem
it is reduced quadratic equation
$$k^{2} + k p + q = 0$$
where
$$p = \frac{b}{a}$$
$$p = -4$$
$$q = \frac{c}{a}$$
$$q = 13$$
Vieta Formulas
$$k_{1} + k_{2} = - p$$
$$k_{1} k_{2} = q$$
$$k_{1} + k_{2} = 4$$
$$k_{1} k_{2} = 13$$
$$k^{2} + k p + q = 0$$
where
$$p = \frac{b}{a}$$
$$p = -4$$
$$q = \frac{c}{a}$$
$$q = 13$$
Vieta Formulas
$$k_{1} + k_{2} = - p$$
$$k_{1} k_{2} = q$$
$$k_{1} + k_{2} = 4$$
$$k_{1} k_{2} = 13$$
Sum and product of roots
[src]
sum
0 + 2 - 3*I + 2 + 3*I
$$\left(0 + \left(2 - 3 i\right)\right) + \left(2 + 3 i\right)$$
=
4
$$4$$
product
1*(2 - 3*I)*(2 + 3*I)
$$1 \cdot \left(2 - 3 i\right) \left(2 + 3 i\right)$$
=
13
$$13$$
13
The graph
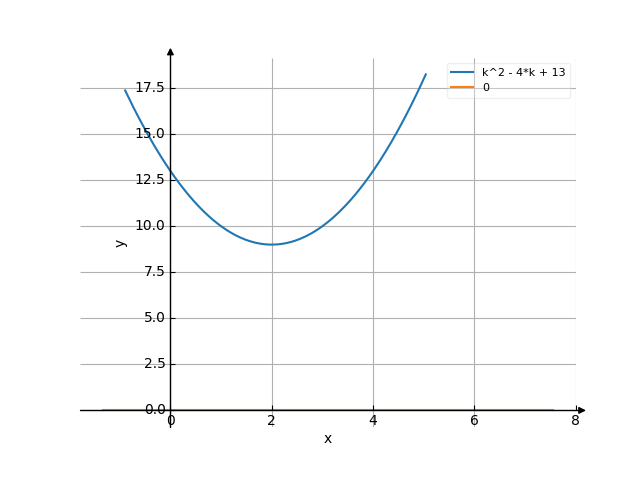

![Solve the equation k²-4*k+13=0 (k squared minus 4 multiply by k plus 13 equally 0) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] k^2-4*k+13=0](/media/krcore-image-pods/176/hash/equation/6/6e/43b8894f9b6cd2e7326da25e56ae2.png)
 Equation 3*9^(x-1/2)-7*6^x+3*4^(x+1)=0
Equation 3*9^(x-1/2)-7*6^x+3*4^(x+1)=0
 Equation 12-x^2=11
Equation 12-x^2=11
 Equation 3*x^2-3=0
Equation 3*x^2-3=0
 Equation k^2-4*k+13=0
Equation k^2-4*k+13=0