You entered:
cos(x+pi/3)=(-1)/sqrt(2)
What you mean?
cos(x+pi/3)=(-1)/sqrt(2) equation
The teacher will be very surprised to see your correct solution 😉
The solution
You have entered
[src]
/ pi\ -1
cos|x + --| = -----
\ 3 / ___
\/ 2
$$\cos{\left(x + \frac{\pi}{3} \right)} = - \frac{1}{\sqrt{2}}$$
Detail solution
Given the equation
$$\cos{\left(x + \frac{\pi}{3} \right)} = - \frac{1}{\sqrt{2}}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x + \frac{\pi}{3} = 2 \pi n + \operatorname{acos}{\left(- \frac{\sqrt{2}}{2} \right)}$$
$$x + \frac{\pi}{3} = 2 \pi n - \pi + \operatorname{acos}{\left(- \frac{\sqrt{2}}{2} \right)}$$
Or
$$x + \frac{\pi}{3} = 2 \pi n + \frac{3 \pi}{4}$$
$$x + \frac{\pi}{3} = 2 \pi n - \frac{\pi}{4}$$
, where n - is a integer
Move
$$\frac{\pi}{3}$$
to right part of the equation with the opposite sign, in total:
$$x = 2 \pi n + \frac{5 \pi}{12}$$
$$x = 2 \pi n - \frac{7 \pi}{12}$$
$$\cos{\left(x + \frac{\pi}{3} \right)} = - \frac{1}{\sqrt{2}}$$
- this is the simplest trigonometric equation
This equation is transformed to
$$x + \frac{\pi}{3} = 2 \pi n + \operatorname{acos}{\left(- \frac{\sqrt{2}}{2} \right)}$$
$$x + \frac{\pi}{3} = 2 \pi n - \pi + \operatorname{acos}{\left(- \frac{\sqrt{2}}{2} \right)}$$
Or
$$x + \frac{\pi}{3} = 2 \pi n + \frac{3 \pi}{4}$$
$$x + \frac{\pi}{3} = 2 \pi n - \frac{\pi}{4}$$
, where n - is a integer
Move
$$\frac{\pi}{3}$$
to right part of the equation with the opposite sign, in total:
$$x = 2 \pi n + \frac{5 \pi}{12}$$
$$x = 2 \pi n - \frac{7 \pi}{12}$$
Rapid solution
[src]
5*pi
x_1 = ----
12
$$x_{1} = \frac{5 \pi}{12}$$
11*pi
x_2 = -----
12
$$x_{2} = \frac{11 \pi}{12}$$
Sum and product of roots
[src]
sum
5*pi 11*pi ---- + ----- 12 12
$$\left(\frac{5 \pi}{12}\right) + \left(\frac{11 \pi}{12}\right)$$
=
4*pi ---- 3
$$\frac{4 \pi}{3}$$
product
5*pi 11*pi ---- * ----- 12 12
$$\left(\frac{5 \pi}{12}\right) * \left(\frac{11 \pi}{12}\right)$$
=
2 55*pi ------ 144
$$\frac{55 \pi^{2}}{144}$$
Numerical answer
[src]
x1 = 725.446103591443
x2 = -91.3679863419031
x3 = 71.9948316447661
x4 = -97.6511716490827
x5 = 9.16297857297023
x6 = 57.857664703612
x7 = 32.7249234748937
x8 = 40.5789051088682
x9 = -1871.08022460052
x10 = 34.2957198016886
x11 = 90.8443875663049
x12 = -78.801615727544
x13 = 59.4284610304069
x14 = 65.7116463375865
x15 = -34.8193185772869
x16 = -42.6733002112614
x17 = -36.3901149040818
x18 = -15.9697626557481
x19 = 51.5744793964324
x20 = -48.9564855184409
x21 = -85.0848010347236
x22 = -92.9387826686981
x23 = -41.1025038844665
x24 = 20.1585528605345
x25 = -4.97418836818384
x26 = 70.4240353179712
x27 = 7.59218224617533
x28 = 158.388629618485
x29 = -11.2573736753634
x30 = 46.8620904160477
x31 = -61.5228561328001
x32 = -59.9520598060052
x33 = -17.540558982543
x34 = -47.3856891916461
x35 = -55.2396708256205
x36 = -67.8060414399797
x37 = 15.4461638801498
x38 = 13.8753675533549
x39 = 45.2912940892529
x40 = -28.5361332701073
x41 = -99.2219679758776
x42 = 76.7072206251508
x43 = 53.1452757232273
x44 = 2.87979326579064
x45 = 89.27359123951
x46 = -74.0892267471593
x47 = -53.6688744988256
x48 = -22.2529479629277
x49 = -9.68657734856853
x50 = 21.7293491873294
x51 = 78.2780169519457
x52 = 415.999227212848
x53 = 101.839961853869
x54 = 26.4417381677141
x55 = -80.3724120543389
x56 = -86.6555973615185
x57 = -3.40339204138894
x58 = -66.2352451131848
x59 = -23.8237442897226
x60 = 1.30899693899575
x61 = 64.1408500107916
x62 = 82.9904059323304
x63 = 84.5612022591253
x64 = -72.5184304203644
x65 = 95.5567765466895
x66 = 951.640774649908
x67 = -30.1069295969022
x68 = 97.1275728734844
x69 = 39.0081087820733
x70 = 28.012534494509
x70 = 28.012534494509
The graph
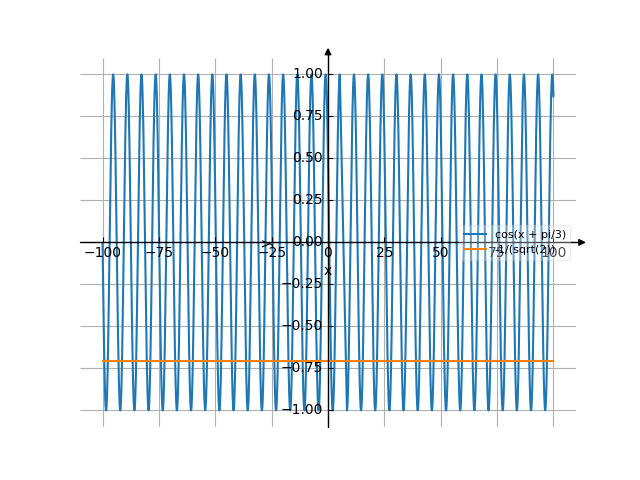

![Solve the equation cos(x+pi/3)=(-1)/sqrt(2) (co sinus of e of (x plus Pi divide by 3) equally (minus 1) divide by square root of (2)) - Find the roots of the equation in detail step by step. [THERE'S THE ANSWER!] cos(x+pi/3)=(-1)/sqrt(2)](/media/krcore-image-pods/176/hash/equation/8/18/867f36f4657ae938a02b511098920.png)
 Equation cos(x+pi/3)=(-1)/sqrt(2)
Equation cos(x+pi/3)=(-1)/sqrt(2)
 Equation sin^2x=1/2
Equation sin^2x=1/2
 Equation tg2x-1=0
Equation tg2x-1=0
 Equation sin(8*x-pi/3)=0
Equation sin(8*x-pi/3)=0
 cos(x+pi/3)
cos(x+pi/3)