Derivative of 1/((x-2)*(x^2-1))

You have entered [src]

         1        
1*----------------
          / 2    \
  (x - 2)*\x  - 1/

1 \cdot \frac{1}{\left(x - 2\right) \left(x^{2} - 1\right)}

d /         1        \
--|1*----------------|
dx|          / 2    \|
  \  (x - 2)*\x  - 1//

\frac{d}{d x} 1 \cdot \frac{1}{\left(x - 2\right) \left(x^{2} - 1\right)}

Transform

Detail solution

Apply the quotient rule, which is:

$\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$

$f{\left(x \right)} = 1$ and $g{\left(x \right)} = \left(x - 2\right) \left(x^{2} - 1\right)$ .

To find $\frac{d}{d x} f{\left(x \right)}$ :
1. The derivative of the constant $1$ is zero.
To find $\frac{d}{d x} g{\left(x \right)}$ :
1. Apply the product rule:
  
  $\frac{d}{d x} f{\left(x \right)} g{\left(x \right)} = f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}$
  
  $f{\left(x \right)} = x^{2} - 1$ ; to find $\frac{d}{d x} f{\left(x \right)}$ :
  1. Differentiate $x^{2} - 1$ term by term:
    1. The derivative of the constant $-1$ is zero.
    2. Apply the power rule: $x^{2}$ goes to $2 x$
    The result is: $2 x$
  $g{\left(x \right)} = x - 2$ ; to find $\frac{d}{d x} g{\left(x \right)}$ :
  1. Differentiate $x - 2$ term by term:
    1. The derivative of the constant $-2$ is zero.
    2. Apply the power rule: $x$ goes to $1$
    The result is: $1$
  The result is: $x^{2} + 2 x \left(x - 2\right) - 1$
Now plug in to the quotient rule:

$\frac{- x^{2} - 2 x \left(x - 2\right) + 1}{\left(x - 2\right)^{2} \left(x^{2} - 1\right)^{2}}$

The answer is:

\frac{- x^{2} - 2 x \left(x - 2\right) + 1}{\left(x - 2\right)^{2} \left(x^{2} - 1\right)^{2}}

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

       1         /     2              \
----------------*\1 - x  - 2*x*(x - 2)/
        / 2    \                       
(x - 2)*\x  - 1/                       
---------------------------------------
                    / 2    \           
            (x - 2)*\x  - 1/

\frac{\frac{1}{\left(x - 2\right) \left(x^{2} - 1\right)} \left(- x^{2} - 2 x \left(x - 2\right) + 1\right)}{\left(x - 2\right) \left(x^{2} - 1\right)}

Simplify

The second derivative [src]

                2                                                                    /      2               \
          -1 + x  + 2*x*(-2 + x)   /  1        2*x  \ /      2               \   2*x*\-1 + x  + 2*x*(-2 + x)/
4 - 6*x + ---------------------- + |------ + -------|*\-1 + x  + 2*x*(-2 + x)/ + ----------------------------
                  -2 + x           |-2 + x         2|                                            2           
                                   \         -1 + x /                                      -1 + x            
-------------------------------------------------------------------------------------------------------------
                                                      2                                                      
                                             /      2\          2                                            
                                             \-1 + x / *(-2 + x)

\frac{- 6 x + \frac{2 x \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x^{2} - 1} + \left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) \left(x^{2} + 2 x \left(x - 2\right) - 1\right) + 4 + \frac{x^{2} + 2 x \left(x - 2\right) - 1}{x - 2}}{\left(x - 2\right)^{2} \left(x^{2} - 1\right)^{2}}

Simplify

The third derivative [src]

 /                                                                                                                                                                                                    /  1        2*x  \ /      2               \                                                          /  1        2*x  \ /      2               \                               \ 
 |                                                                                                                                                                                                    |------ + -------|*\-1 + x  + 2*x*(-2 + x)/                                                      2*x*|------ + -------|*\-1 + x  + 2*x*(-2 + x)/                               | 
 |                     /      2               \                                                                /                            2                        \     /      2               \   |-2 + x         2|                                                  2 /      2               \       |-2 + x         2|                                /      2               \| 
 |    6*(-2 + 3*x)   2*\-1 + x  + 2*x*(-2 + x)/                /  1        2*x  \     /      2               \ |    1          1         4*x              2*x        |   3*\-1 + x  + 2*x*(-2 + x)/   \         -1 + x /                            12*x*(-2 + 3*x)   12*x *\-1 + x  + 2*x*(-2 + x)/       \         -1 + x /                            8*x*\-1 + x  + 2*x*(-2 + x)/| 
-|6 - ------------ - -------------------------- - 2*(-2 + 3*x)*|------ + -------| + 2*\-1 + x  + 2*x*(-2 + x)/*|--------- - ------- + ---------- + ------------------| + -------------------------- + ------------------------------------------- - --------------- + ------------------------------ + ----------------------------------------------- + ----------------------------| 
 |       -2 + x                     2                          |-2 + x         2|                              |        2         2            2   /      2\         |                   2                               -2 + x                               2                          2                                       2                            /      2\              | 
 |                            -1 + x                           \         -1 + x /                              |(-2 + x)    -1 + x    /      2\    \-1 + x /*(-2 + x)|           (-2 + x)                                                               -1 + x                  /      2\                                  -1 + x                             \-1 + x /*(-2 + x)     | 
 \                                                                                                             \                      \-1 + x /                      /                                                                                                          \-1 + x /                                                                                            / 
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
                                                                                                                                                                                           2                                                                                                                                                                                           
                                                                                                                                                                                  /      2\          2                                                                                                                                                                                 
                                                                                                                                                                                  \-1 + x / *(-2 + x)

- \frac{\frac{12 x^{2} \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x^{2} - 1\right)^{2}} - \frac{12 x \left(3 x - 2\right)}{x^{2} - 1} + \frac{2 x \left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x^{2} - 1} + \frac{8 x \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x - 2\right) \left(x^{2} - 1\right)} - 2 \cdot \left(3 x - 2\right) \left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) + 2 \left(x^{2} + 2 x \left(x - 2\right) - 1\right) \left(\frac{4 x^{2}}{\left(x^{2} - 1\right)^{2}} + \frac{2 x}{\left(x - 2\right) \left(x^{2} - 1\right)} - \frac{1}{x^{2} - 1} + \frac{1}{\left(x - 2\right)^{2}}\right) + 6 - \frac{2 \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x^{2} - 1} - \frac{6 \cdot \left(3 x - 2\right)}{x - 2} + \frac{\left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x - 2} + \frac{3 \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x - 2\right)^{2}}}{\left(x - 2\right)^{2} \left(x^{2} - 1\right)^{2}}

Simplify

3-я производная [src]

 /                                                                                                                                                                                                    /  1        2*x  \ /      2               \                                                          /  1        2*x  \ /      2               \                               \ 
 |                                                                                                                                                                                                    |------ + -------|*\-1 + x  + 2*x*(-2 + x)/                                                      2*x*|------ + -------|*\-1 + x  + 2*x*(-2 + x)/                               | 
 |                     /      2               \                                                                /                            2                        \     /      2               \   |-2 + x         2|                                                  2 /      2               \       |-2 + x         2|                                /      2               \| 
 |    6*(-2 + 3*x)   2*\-1 + x  + 2*x*(-2 + x)/                /  1        2*x  \     /      2               \ |    1          1         4*x              2*x        |   3*\-1 + x  + 2*x*(-2 + x)/   \         -1 + x /                            12*x*(-2 + 3*x)   12*x *\-1 + x  + 2*x*(-2 + x)/       \         -1 + x /                            8*x*\-1 + x  + 2*x*(-2 + x)/| 
-|6 - ------------ - -------------------------- - 2*(-2 + 3*x)*|------ + -------| + 2*\-1 + x  + 2*x*(-2 + x)/*|--------- - ------- + ---------- + ------------------| + -------------------------- + ------------------------------------------- - --------------- + ------------------------------ + ----------------------------------------------- + ----------------------------| 
 |       -2 + x                     2                          |-2 + x         2|                              |        2         2            2   /      2\         |                   2                               -2 + x                               2                          2                                       2                            /      2\              | 
 |                            -1 + x                           \         -1 + x /                              |(-2 + x)    -1 + x    /      2\    \-1 + x /*(-2 + x)|           (-2 + x)                                                               -1 + x                  /      2\                                  -1 + x                             \-1 + x /*(-2 + x)     | 
 \                                                                                                             \                      \-1 + x /                      /                                                                                                          \-1 + x /                                                                                            / 
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
                                                                                                                                                                                           2                                                                                                                                                                                           
                                                                                                                                                                                  /      2\          2                                                                                                                                                                                 
                                                                                                                                                                                  \-1 + x / *(-2 + x)

- \frac{\frac{12 x^{2} \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x^{2} - 1\right)^{2}} - \frac{12 x \left(3 x - 2\right)}{x^{2} - 1} + \frac{2 x \left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x^{2} - 1} + \frac{8 x \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x - 2\right) \left(x^{2} - 1\right)} - 2 \cdot \left(3 x - 2\right) \left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) + 2 \left(x^{2} + 2 x \left(x - 2\right) - 1\right) \left(\frac{4 x^{2}}{\left(x^{2} - 1\right)^{2}} + \frac{2 x}{\left(x - 2\right) \left(x^{2} - 1\right)} - \frac{1}{x^{2} - 1} + \frac{1}{\left(x - 2\right)^{2}}\right) + 6 - \frac{2 \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x^{2} - 1} - \frac{6 \cdot \left(3 x - 2\right)}{x - 2} + \frac{\left(\frac{2 x}{x^{2} - 1} + \frac{1}{x - 2}\right) \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{x - 2} + \frac{3 \left(x^{2} + 2 x \left(x - 2\right) - 1\right)}{\left(x - 2\right)^{2}}}{\left(x - 2\right)^{2} \left(x^{2} - 1\right)^{2}}

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

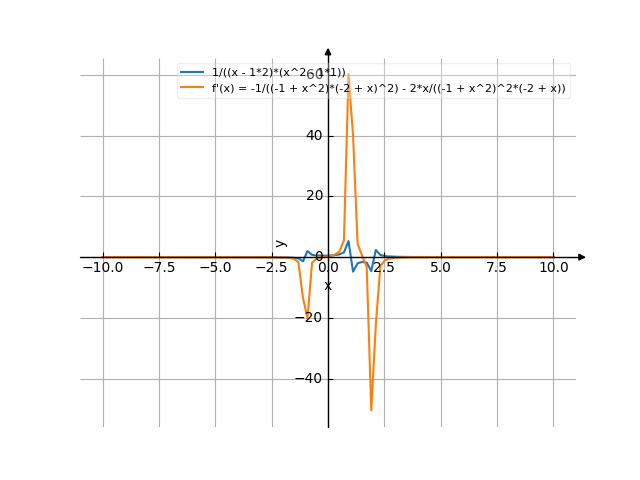
Derivative of 1/((x-2)*(x^2-1))

The graph:

Piecewise:

The solution