Derivative of arccos(sqrt(2)/x)+1/sqrt(2)*(x*sqrt(x*x-2))
The solution
You have entered
[src]
/ ___\
|\/ 2 | 1 _________
acos|-----| + 1*-----*x*\/ x*x - 2
\ x / ___
\/ 2
$$1 \cdot \frac{1}{\sqrt{2}} x \sqrt{x x - 2} + \operatorname{acos}{\left(\frac{\sqrt{2}}{x} \right)}$$
/ / ___\ \ d | |\/ 2 | 1 _________| --|acos|-----| + 1*-----*x*\/ x*x - 2 | dx| \ x / ___ | \ \/ 2 /
$$\frac{d}{d x} \left(1 \cdot \frac{1}{\sqrt{2}} x \sqrt{x x - 2} + \operatorname{acos}{\left(\frac{\sqrt{2}}{x} \right)}\right)$$
The first derivative
[src]
___
2 \/ 2
___ ___ x *-----
_________ \/ 2 \/ 2 2
\/ x*x - 2 *----- + ---------------- + -----------
2 ________ _________
2 / 2 \/ x*x - 2
x * / 1 - --
/ 2
\/ x
$$\frac{\frac{\sqrt{2}}{2} x^{2}}{\sqrt{x x - 2}} + \frac{\sqrt{2}}{2} \sqrt{x x - 2} + \frac{\sqrt{2}}{x^{2} \sqrt{1 - \frac{2}{x^{2}}}}$$
The second derivative
[src]
/ 3 \
___ | 2 2 x 3*x |
\/ 2 *|- -------------- - ---------------- - -------------- + --------------|
| 3/2 ________ 3/2 _________|
| 5 / 2 \ 3 / 2 / 2\ / 2 |
| x *|1 - --| x * / 1 - -- 2*\-2 + x / 2*\/ -2 + x |
| | 2| / 2 |
\ \ x / \/ x /
$$\sqrt{2} \left(- \frac{x^{3}}{2 \left(x^{2} - 2\right)^{\frac{3}{2}}} + \frac{3 x}{2 \sqrt{x^{2} - 2}} - \frac{2}{x^{3} \sqrt{1 - \frac{2}{x^{2}}}} - \frac{2}{x^{5} \left(1 - \frac{2}{x^{2}}\right)^{\frac{3}{2}}}\right)$$
The third derivative
[src]
/ 2 4 \
___ | 3 3*x 6 12 14 3*x |
\/ 2 *|-------------- - ------------ + ---------------- + -------------- + -------------- + --------------|
| _________ 3/2 ________ 5/2 3/2 5/2|
| / 2 / 2\ 4 / 2 8 / 2 \ 6 / 2 \ / 2\ |
|2*\/ -2 + x \-2 + x / x * / 1 - -- x *|1 - --| x *|1 - --| 2*\-2 + x / |
| / 2 | 2| | 2| |
\ \/ x \ x / \ x / /
$$\sqrt{2} \cdot \left(\frac{3 x^{4}}{2 \left(x^{2} - 2\right)^{\frac{5}{2}}} - \frac{3 x^{2}}{\left(x^{2} - 2\right)^{\frac{3}{2}}} + \frac{3}{2 \sqrt{x^{2} - 2}} + \frac{6}{x^{4} \sqrt{1 - \frac{2}{x^{2}}}} + \frac{14}{x^{6} \left(1 - \frac{2}{x^{2}}\right)^{\frac{3}{2}}} + \frac{12}{x^{8} \left(1 - \frac{2}{x^{2}}\right)^{\frac{5}{2}}}\right)$$
The graph
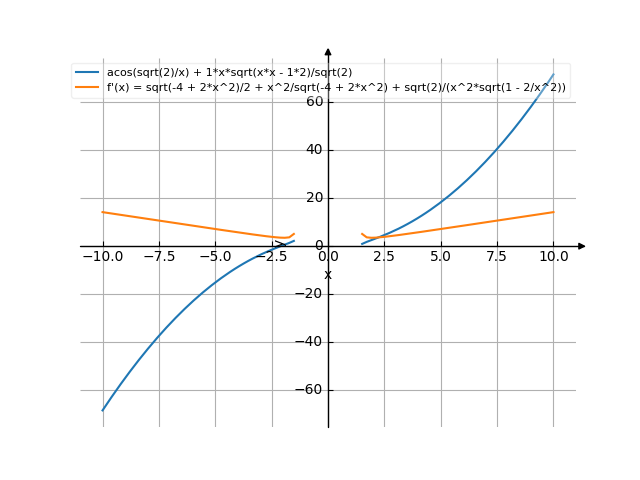

![Find the derivative of y' = f'(x) = arccos(sqrt(2)/x)+1/sqrt(2)*(x*sqrt(x*x-2)) (arc co sinus of e of (square root of (2) divide by x) plus 1 divide by square root of (2) multiply by (x multiply by square root of (x multiply by x minus 2))) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] arccos(sqrt(2)/x)+1/sqrt(2)*(x*sqrt(x*x-2))](/media/krcore-image-pods/176/hash/derivative/8/f7/c2133a1e3fa9498bfd91b91d3b219.png)
 Derivative of x/(e^x+1)
Derivative of x/(e^x+1)
 Derivative of (x^2-1)/((2*x))
Derivative of (x^2-1)/((2*x))
 Derivative of ((x-1)/(x+1))^4
Derivative of ((x-1)/(x+1))^4
 Derivative of (x-1)/(2*x+3)
Derivative of (x-1)/(2*x+3)