Derivative of 8sin5x
The solution
You have entered
[src]
8*sin(5*x)
$$8 \sin{\left(5 x \right)}$$
d --(8*sin(5*x)) dx
$$\frac{d}{d x} 8 \sin{\left(5 x \right)}$$
Detail solution
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Let .
-
The derivative of sine is cosine:
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
So, the result is:
The answer is:
The graph
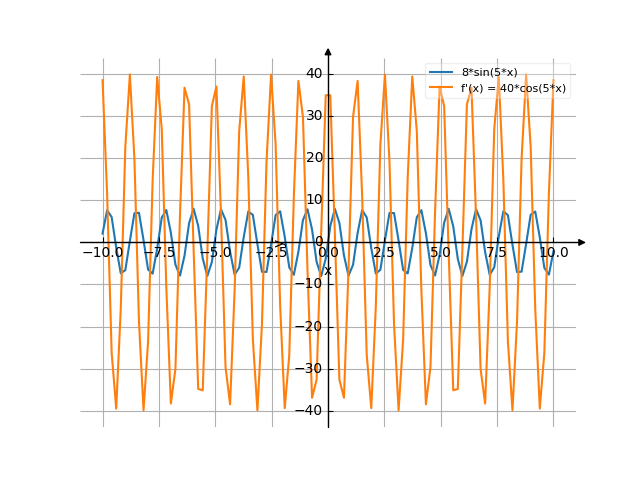

![Find the derivative of y' = f'(x) = 8sin5x (8 sinus of 5x) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] 8sin5x](/media/krcore-image-pods/176/hash/derivative/9/c5/8148dc82e4b252efb9304b404eedd.png)
 Derivative of 2*x^4
Derivative of 2*x^4
 Derivative of sinx/cosx
Derivative of sinx/cosx
 Derivative of sin(x)*sin(x)
Derivative of sin(x)*sin(x)
 Derivative of sin(2*x+3)
Derivative of sin(2*x+3)