Doppeltes Integral Schritt für Schritt

Mit der richtigen Integral-Lösung wirst du der/die Beliebteste in der Gruppe ❤️😊

Was kann es?

• Berechnet das doppelte Integral über ein durch angegebene Kurven begrenztes Gebiet (hier), und bestimmt dabei die Integrationsgrenzen hier
• Berechnet mit dem doppelten Integral die Fläche der durch Kurven begrenzten Figur
• Berechnet iterierte Integrale (mit bereits bekannten Grenzen)
• Schreibt das doppelte Integral von f(x, y) als iteriertes Integral
• Berechnet die Masse einer Platte über ein doppeltes Integral
• Vertauschung der Integrationsreihenfolge im iterierten Integral (hier)
• Wo es sinnvoll ist polar Koordinaten, werden sie verwendet

Flächenberechnung

Zur Flächenberechnung setzen Sie im Integranden einfach 1 ein. Sie können auch den folgenden Rechner verwenden: Fläche zwischen Kurven

Beispiele für doppelte Integrale

Wie man das Gebiet D angibt?

Das Gebiet D kann auf verschiedene Weise angegeben werden:

• Durch Kurven:
  1. Kreis
  2. Zwei Kreise
  3. Ellipse
  4. Parabel
  5. Weitere
• Über Eckpunkte:
  1. Dreieck

     A(0, 1)

     B(1, 0)

     C(0, 0)

  2. Quadrat
  3. Rechteck
• und — Quadrant

Als Ungleichung

Geben Sie das Gebiet durch Ungleichungen an:

x > pi/2

-1/2 < y <= 3/2

x < sqrt(2)/2 + 1

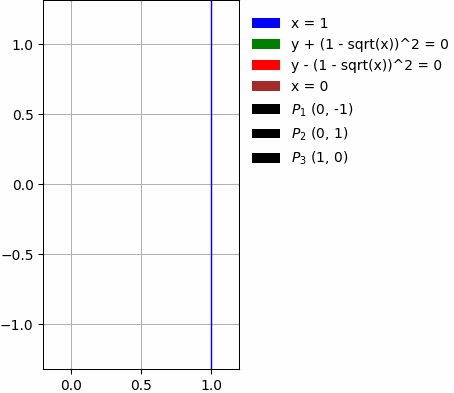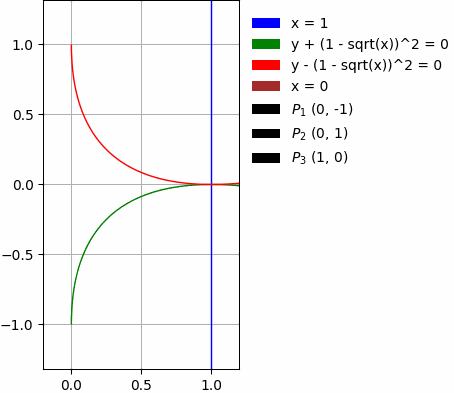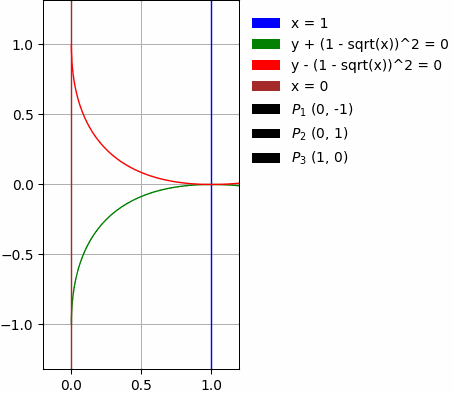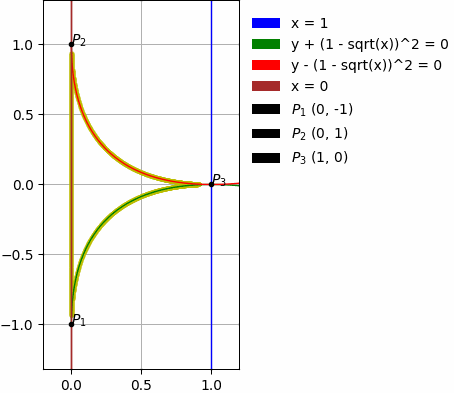
Die oben genannten Beispiele enthalten außerdem:

• Betrag oder absoluter Wert: absolute(x) oder |x|
• Quadratwurzeln sqrt(x),
  Kubikwurzeln cbrt(x)
• trigonometrische Funktionen:
  Sinus sin(x), Kosinus cos(x), Tangens tan(x), Kotangens ctan(x)
• Exponentialfunktionen exp(x)
• umkehrtrigonometrische Funktionen:
  Arkussinus asin(x), Arkuskosinus acos(x), Arkustangens atan(x), Arkuskotangens acot(x)
• natürliche Logarithmen ln(x),
  Zehnerlogarithmen log(x)
• hyperbolische Funktionen:
  Hyperbelsinus sh(x), Hyperbelkosinus ch(x), Hyperbeltangens und -kotangens tanh(x), ctanh(x)
• inverse hyperbolische Funktionen:
  Hyperbel‑Arkussinus asinh(x), Hyperbel‑Arkus kosinus acosh(x), Hyperbel‑Arkustangens atanh(x), Hyperbel‑Arkuskotangens acoth(x)
• weitere trigonometrische und hyperbolische Funktionen:
  Sekans sec(x), Kosekans csc(x), Arkussekans asec(x), Arkuskosekans acsc(x), Hyperbelsekans sech(x), Hyperbelkosekans csch(x), Hyperbel‑Arkussekans asech(x), Hyperbel‑Arkuskosekans acsch(x)
• Rundungsfunktionen:
  Abrunden floor(x), Aufrunden ceiling(x)
• Vorzeichen einer Zahl:
  sign(x)
• für die Wahrscheinlichkeitsrechnung:
  Fehlerfunktion erf(x) (Wahrscheinlichkeitsintegral), Laplace‑Funktion laplace(x)
• Fakultät von x:
  x! oder factorial(x)
• Gammafunktion gamma(x)
• Lambert‑W‑Funktion LambertW(x)
• trigonometrische Integrale: Si(x), Ci(x), Shi(x), Chi(x)

Eingaberegeln

Folgende Operationen sind möglich

2*x

- Multiplikation

3/x

- Division

x^2

- Quadrieren

x^3

- Kubieren

x^5

- Potenzieren

x + 7

- Addition

x - 6

- Subtraktion

Reelle Zahlen

eingeben als 7.5, nicht 7,5

Konstanten

pi

- Kreiszahl Pi

e

- Basis des natürlichen Logarithmus

i

- komplexe Zahl

oo

- Unendlichkeitszeichen

Diese Beispiele können auch für obere und untere Grenzen in doppelten Integralen verwendet werden.