In die kanonische Form bringen
Mit der richtigen Lösung wirst du der/die Beliebteste in der Gruppe ❤️😊
Was kann der Kanonische‑Form‑Rechner?
- Ermittelt anhand der gegebenen Gleichung:
- Kanonische Form der Gleichung (für Kurven und Flächen 2. Ordnung)
- Basisvektoren des kanonischen Koordinatensystems (für Kurven 2. Ordnung)
- Zentrum des kanonischen Koordinatensystems (für Kurven 2. Ordnung)
- Ausführliche Lösung auf zwei Arten:
- Direkte Methode mit Verschiebung des Koordinatenursprungs und Rotation um den neuen Ursprung (für Kurven)
- Invariantenmethode mit Berechnung mehrerer Determinanten (für Kurven und Flächen)
- Zeichnet den Graph einer Kurve 2. Ordnung, das Zentrum des kanonischen Systems und die Basisvektoren
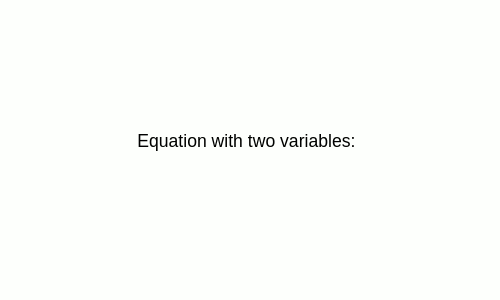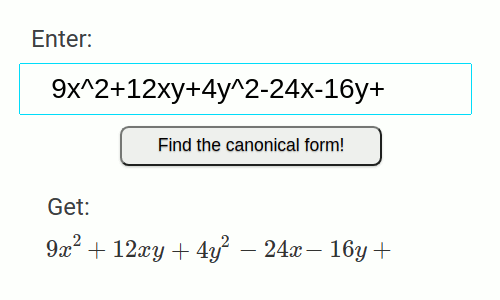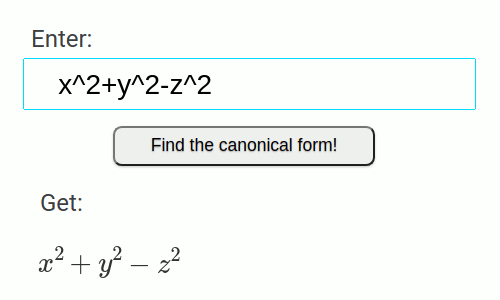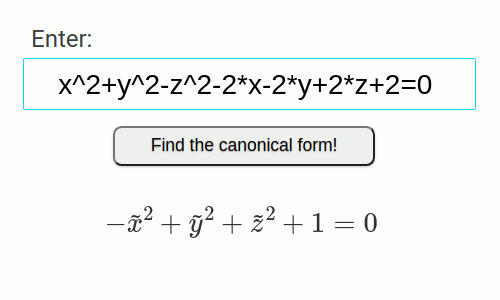
Beispiele
- Zwei parallele Geraden
9x^2+12xy+4y^2-24x-16y+3=0
- Parabel
x^2-2xy+y^2-10x-6y+25=0
- Entartete Ellipse
5x^2+4xy+y^2-6x-2y+2=0
- Ellipse
5*x^2+4*x*y+8*y^2+8*x+14*y+5=0
- Imaginäre Ellipse
8063 - 250*y - 10*x + 50*x^2 + 50*y^2
- Ellipsoid
-243 - 216*z - 18*x + 4*y^2 + 25*x^2 + 36*z^2 + 16*x*y = 0
- Imaginärer Ellipsoid
2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0
- Zweischaliges Hyperboloid
x^2+y^2-z^2-2*x-2*y+2*z+2=0
- Elliptisches Paraboloid
x^2+y^2-6*x+6*y-4*z+18=0
- Zwei parallele Ebenen
x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0
- Gleichung imaginärer sich schneidender Geraden
x^2 + 4*y^2 = 0
- Hyperbelgleichung
xy = 1
- Imaginäre parallele Geraden
x^2 - 2x + 17 = 0
- Zusammenfallende Geraden
x^2 = 0
y^2 = 0
- Kanonische Gleichung des Ellipsoids
x^2/4 + y^2/9 + z^2 = 16
z^2 - 6*z - x/2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 27/4 = 0
- Imaginärer Kegel
z^2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 6*z = 0
- Einschaliges Hyperboloid
x^2/4 - y^2/9 + z^2 = 16
z^2 + x^2/4 + 2*y/9 + 5*y^2/36 - x*y/2 = 145/9
- Kanonische Gleichung des Kegels
x^2/4 - y^2/9 + z^2 = 0
8*y + 36*z^2 + 18*x*y = 4 + 13*y^2 + 9*x^2
- Hyperbolisches Paraboloid
x^2/4 - y^2/9 = 2*z
4*x^2 + 4*z^2 + 2*y = y^2 + 8*x*z + 32*z + 33
xy = z
- Elliptischer Zylinder
16*x^2 + 25*y^2 - 32*x + 50*y - 359 = 0
x^2 + y^2 - 2x - 2y = 7
- Imaginärer elliptischer Zylinder
5*x^2 + 13*y^2 + 70 = 0
25 - 16*y + 4*y^2 + 16*x^2 + 16*z^2 - 32*x*z = 0
- Schneidende Ebenen
x^2 - y^2 = 0
16*x^2 - 25*y^2 + 16*z^2 - 32*x*z + 100*y - 100
- Hyperbolischer Zylinder
4*x^2 - 5*y^2 - 8*x + 20*y = 11
xy = 1
- Schneidende Ebenen
x^2/4 - y^2/16 = 0
-100 - 4*y^2 + 16*x^2 + 16*z^2 + 40*y - 32*x*z
- Parabolischer Zylinder
y^2 = 2x
x^2 = -4y
-z^2/9 = x
y = sqrt(2)/2*z^2
10 + y^2 + z^2 - 2*x - 2*y*z
- Imaginäre parallele Ebenen
x^2 + 1 = 0
y^2 + 4 = 0
16 + 4*z^2 + 9*y^2 + 16*x^2 - 16*x*z - 12*y*z + 24*x*y = 0
- Zusammenfallende Ebenen
y^2 = 0
x^2 = 0
4*x^2 + 9*y^2 + 16*z^2 - 24*y*z - 16*x*z + 12*x*y
Mehr über Kanonische Form
.
Beispiele für Gleichungen von Kurven und Flächen 2. Ordnung
| Gleichung | Kanonische Form | Typ | Dimension |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Zwei parallele Geraden | Linie |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Parabel | Linie |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Entartete Ellipse | Linie |
| 5*x^2+4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Ellipse | Linie |
| 2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0 | z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1 | Imaginärer Ellipsoid | Oberfläche |
| x^2+y^2-z^2-2*x-2*y+2*z+2=0 | x^2/1^2+y^2-z^2=-1 | Zweischaliges Hyperboloid | Oberfläche |
| x^2+y^2-6*x+6*y-4*z+18=0 | x^2/2+y^2-2*z=0 oder x^2/2+y^2+2*z=0 | Elliptisches Paraboloid | Oberfläche |
| x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0 | x^2/=1/14 | Zwei parallele Ebenen | Oberfläche |
