x^2+2x-3 canonical form
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given line equation of 2-order:
$$x^{2} + 2 x - 3 = 0$$
This equation looks like:
$$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$
where
$$a_{11} = 1$$
$$a_{12} = 0$$
$$a_{13} = 1$$
$$a_{22} = 0$$
$$a_{23} = 0$$
$$a_{33} = -3$$
To calculate the determinant
$$\Delta = \left|\begin{matrix}a_{11} & a_{12}\\a_{12} & a_{22}\end{matrix}\right|$$
or, substitute
$$\Delta = \left|\begin{matrix}1 & 0\\0 & 0\end{matrix}\right|$$
$$\Delta = 0$$
Because
$$\Delta$$
is equal to 0, then
$$\left(\tilde x + 1\right)^{2} = 4$$
$$\tilde x'^{2} = 4$$
Given equation is two parallel straight lines
- reduced to canonical form
where replacement made
$$\tilde x' = \tilde x + 1$$
$$\tilde y' = \tilde y$$
The center of the canonical coordinate system in OXY
$$x_{0} = \tilde x \cos{\left(\phi \right)} - \tilde y \sin{\left(\phi \right)}$$
$$y_{0} = \tilde x \sin{\left(\phi \right)} + \tilde y \cos{\left(\phi \right)}$$
$$x_{0} = -1 + 0 \cdot 0$$
$$y_{0} = - 0$$
$$x_{0} = -1$$
$$y_{0} = 0$$
The center of canonical coordinate system at point O
Basis of the canonical coordinate system
$$\vec e_1 = \left( 1, \ 0\right)$$
$$\vec e_2 = \left( 0, \ 1\right)$$
$$x^{2} + 2 x - 3 = 0$$
This equation looks like:
$$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$
where
$$a_{11} = 1$$
$$a_{12} = 0$$
$$a_{13} = 1$$
$$a_{22} = 0$$
$$a_{23} = 0$$
$$a_{33} = -3$$
To calculate the determinant
$$\Delta = \left|\begin{matrix}a_{11} & a_{12}\\a_{12} & a_{22}\end{matrix}\right|$$
or, substitute
$$\Delta = \left|\begin{matrix}1 & 0\\0 & 0\end{matrix}\right|$$
$$\Delta = 0$$
Because
$$\Delta$$
is equal to 0, then
$$\left(\tilde x + 1\right)^{2} = 4$$
$$\tilde x'^{2} = 4$$
Given equation is two parallel straight lines
- reduced to canonical form
where replacement made
$$\tilde x' = \tilde x + 1$$
$$\tilde y' = \tilde y$$
The center of the canonical coordinate system in OXY
$$x_{0} = \tilde x \cos{\left(\phi \right)} - \tilde y \sin{\left(\phi \right)}$$
$$y_{0} = \tilde x \sin{\left(\phi \right)} + \tilde y \cos{\left(\phi \right)}$$
$$x_{0} = -1 + 0 \cdot 0$$
$$y_{0} = - 0$$
$$x_{0} = -1$$
$$y_{0} = 0$$
The center of canonical coordinate system at point O
(-1, 0)
Basis of the canonical coordinate system
$$\vec e_1 = \left( 1, \ 0\right)$$
$$\vec e_2 = \left( 0, \ 1\right)$$
Invariants method
Given line equation of 2-order:
$$x^{2} + 2 x - 3 = 0$$
This equation looks like:
$$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$
where
$$a_{11} = 1$$
$$a_{12} = 0$$
$$a_{13} = 1$$
$$a_{22} = 0$$
$$a_{23} = 0$$
$$a_{33} = -3$$
The invariants of the equation when converting coordinates are determinants:
$$I_{1} = a_{11} + a_{22}$$
$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$
$$I{\left(\lambda \right)} = \left|\begin{matrix}a_{11} - \lambda & a_{12}\\a_{12} & a_{22} - \lambda\end{matrix}\right|$$
substitute coefficients
$$I_{1} = 1$$
$$I_{3} = \left|\begin{matrix}1 & 0 & 1\\0 & 0 & 0\\1 & 0 & -3\end{matrix}\right|$$
$$I{\left(\lambda \right)} = \left|\begin{matrix}1 - \lambda & 0\\0 & - \lambda\end{matrix}\right|$$
$$I_{1} = 1$$
$$I_{2} = 0$$
$$I_{3} = 0$$
$$I{\left(\lambda \right)} = \lambda^{2} - \lambda$$
$$K_{2} = -4$$
Because
$$I_{2} = 0 \wedge I_{3} = 0 \wedge K_{2} < 0 \wedge I_{1} \neq 0$$
then by line type:
this equation is of type : two parallel lines
$$I_{1} \tilde y^{2} + \frac{K_{2}}{I_{1}} = 0$$
or
$$\tilde y^{2} - 4 = 0$$
- reduced to canonical form
$$x^{2} + 2 x - 3 = 0$$
This equation looks like:
$$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$
where
$$a_{11} = 1$$
$$a_{12} = 0$$
$$a_{13} = 1$$
$$a_{22} = 0$$
$$a_{23} = 0$$
$$a_{33} = -3$$
The invariants of the equation when converting coordinates are determinants:
$$I_{1} = a_{11} + a_{22}$$
|a11 a12|
I2 = | |
|a12 a22|$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$
$$I{\left(\lambda \right)} = \left|\begin{matrix}a_{11} - \lambda & a_{12}\\a_{12} & a_{22} - \lambda\end{matrix}\right|$$
|a11 a13| |a22 a23|
K2 = | | + | |
|a13 a33| |a23 a33|substitute coefficients
$$I_{1} = 1$$
|1 0|
I2 = | |
|0 0|$$I_{3} = \left|\begin{matrix}1 & 0 & 1\\0 & 0 & 0\\1 & 0 & -3\end{matrix}\right|$$
$$I{\left(\lambda \right)} = \left|\begin{matrix}1 - \lambda & 0\\0 & - \lambda\end{matrix}\right|$$
|1 1 | |0 0 |
K2 = | | + | |
|1 -3| |0 -3|$$I_{1} = 1$$
$$I_{2} = 0$$
$$I_{3} = 0$$
$$I{\left(\lambda \right)} = \lambda^{2} - \lambda$$
$$K_{2} = -4$$
Because
$$I_{2} = 0 \wedge I_{3} = 0 \wedge K_{2} < 0 \wedge I_{1} \neq 0$$
then by line type:
this equation is of type : two parallel lines
$$I_{1} \tilde y^{2} + \frac{K_{2}}{I_{1}} = 0$$
or
$$\tilde y^{2} - 4 = 0$$
None
- reduced to canonical form

 x^2/36-y^2=1
x^2/36-y^2=1
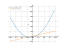 x^2+2x-3
x^2+2x-3
 x^2+2x-3
x^2+2x-3
 x^2+2x-3
x^2+2x-3