16x+32y-212,479=0; 32x+128y-791,249=0
The solution
You have entered
[src]
212479
16*x + 32*y - ------ = 0
1000
$$16 x + 32 y - \frac{212479}{1000} = 0$$
791249
32*x + 128*y - ------ = 0
1000
$$32 x + 128 y - \frac{791249}{1000} = 0$$
or
$$\begin{cases}16 x + 32 y - \frac{212479}{1000} = 0\\32 x + 128 y - \frac{791249}{1000} = 0\end{cases}$$
Detail solution
Given the system of equations
$$16 x + 32 y - \frac{212479}{1000} = 0$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
Let's express from equation 1 x
$$16 x + 32 y - \frac{212479}{1000} = 0$$
Let's move the summand with the variable y from the left part to the right part performing the sign change
$$16 x - \frac{212479}{1000} = \left(- 32 y - \frac{212479}{1000} + \frac{212479}{1000}\right) + 0$$
$$16 x - \frac{212479}{1000} = - 32 y$$
We move the free summand -212479/1000 from the left part to the right part performing the sign change
$$16 x = - 32 y + \frac{212479}{1000}$$
$$16 x = - 32 y + \frac{212479}{1000}$$
Let's divide both parts of the equation by the multiplier of x
$$\frac{16 x}{16} = \frac{- 32 y + \frac{212479}{1000}}{16}$$
$$x = - 2 y + \frac{212479}{16000}$$
Let's try the obtained element x to 2-th equation
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We get:
$$128 y + 32 \cdot \left(- 2 y + \frac{212479}{16000}\right) - \frac{791249}{1000} = 0$$
$$64 y - \frac{366291}{1000} = 0$$
We move the free summand -366291/1000 from the left part to the right part performing the sign change
$$64 y = 0 + \frac{366291}{1000}$$
$$64 y = \frac{366291}{1000}$$
Let's divide both parts of the equation by the multiplier of y
$$\frac{64 y}{64} = \frac{366291}{64 \cdot 1000}$$
$$y = \frac{366291}{64000}$$
Because
$$x = - 2 y + \frac{212479}{16000}$$
then
$$x = \left(-2\right) \frac{366291}{64000} + \frac{212479}{16000}$$
$$x = \frac{58667}{32000}$$
The answer:
$$x = \frac{58667}{32000}$$
$$y = \frac{366291}{64000}$$
$$16 x + 32 y - \frac{212479}{1000} = 0$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
Let's express from equation 1 x
$$16 x + 32 y - \frac{212479}{1000} = 0$$
Let's move the summand with the variable y from the left part to the right part performing the sign change
$$16 x - \frac{212479}{1000} = \left(- 32 y - \frac{212479}{1000} + \frac{212479}{1000}\right) + 0$$
$$16 x - \frac{212479}{1000} = - 32 y$$
We move the free summand -212479/1000 from the left part to the right part performing the sign change
$$16 x = - 32 y + \frac{212479}{1000}$$
$$16 x = - 32 y + \frac{212479}{1000}$$
Let's divide both parts of the equation by the multiplier of x
$$\frac{16 x}{16} = \frac{- 32 y + \frac{212479}{1000}}{16}$$
$$x = - 2 y + \frac{212479}{16000}$$
Let's try the obtained element x to 2-th equation
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We get:
$$128 y + 32 \cdot \left(- 2 y + \frac{212479}{16000}\right) - \frac{791249}{1000} = 0$$
$$64 y - \frac{366291}{1000} = 0$$
We move the free summand -366291/1000 from the left part to the right part performing the sign change
$$64 y = 0 + \frac{366291}{1000}$$
$$64 y = \frac{366291}{1000}$$
Let's divide both parts of the equation by the multiplier of y
$$\frac{64 y}{64} = \frac{366291}{64 \cdot 1000}$$
$$y = \frac{366291}{64000}$$
Because
$$x = - 2 y + \frac{212479}{16000}$$
then
$$x = \left(-2\right) \frac{366291}{64000} + \frac{212479}{16000}$$
$$x = \frac{58667}{32000}$$
The answer:
$$x = \frac{58667}{32000}$$
$$y = \frac{366291}{64000}$$
Rapid solution
Cramer's rule
$$16 x + 32 y - \frac{212479}{1000} = 0$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We give the system of equations to the canonical form
$$16 x + 32 y = \frac{212479}{1000}$$
$$32 x + 128 y = \frac{791249}{1000}$$
Rewrite the system of linear equations as the matrix form
$$\left[\begin{matrix}16 x_{1} + 32 x_{2}\\32 x_{1} + 128 x_{2}\end{matrix}\right] = \left[\begin{matrix}\frac{212479}{1000}\\\frac{791249}{1000}\end{matrix}\right]$$
- this is the system of equations that has the form
A*x = B
Let´s find a solution of this matrix equations using Cramer´s rule:
Since the determinant of the matrix:
$$A = \operatorname{det}{\left(\left[\begin{matrix}16 & 32\\32 & 128\end{matrix}\right] \right)} = 1024$$
, then
The root xi is obtained by dividing the determinant of the matrix Ai. by the determinant of the matrix A.
( Ai we get it by replacement in the matrix A i-th column with column B )
$$x_{1} = \frac{\operatorname{det}{\left(\left[\begin{matrix}\frac{212479}{1000} & 32\\\frac{791249}{1000} & 128\end{matrix}\right] \right)}}{1024} = \frac{58667}{32000}$$
$$x_{2} = \frac{\operatorname{det}{\left(\left[\begin{matrix}16 & \frac{212479}{1000}\\32 & \frac{791249}{1000}\end{matrix}\right] \right)}}{1024} = \frac{366291}{64000}$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We give the system of equations to the canonical form
$$16 x + 32 y = \frac{212479}{1000}$$
$$32 x + 128 y = \frac{791249}{1000}$$
Rewrite the system of linear equations as the matrix form
$$\left[\begin{matrix}16 x_{1} + 32 x_{2}\\32 x_{1} + 128 x_{2}\end{matrix}\right] = \left[\begin{matrix}\frac{212479}{1000}\\\frac{791249}{1000}\end{matrix}\right]$$
- this is the system of equations that has the form
A*x = B
Let´s find a solution of this matrix equations using Cramer´s rule:
Since the determinant of the matrix:
$$A = \operatorname{det}{\left(\left[\begin{matrix}16 & 32\\32 & 128\end{matrix}\right] \right)} = 1024$$
, then
The root xi is obtained by dividing the determinant of the matrix Ai. by the determinant of the matrix A.
( Ai we get it by replacement in the matrix A i-th column with column B )
$$x_{1} = \frac{\operatorname{det}{\left(\left[\begin{matrix}\frac{212479}{1000} & 32\\\frac{791249}{1000} & 128\end{matrix}\right] \right)}}{1024} = \frac{58667}{32000}$$
$$x_{2} = \frac{\operatorname{det}{\left(\left[\begin{matrix}16 & \frac{212479}{1000}\\32 & \frac{791249}{1000}\end{matrix}\right] \right)}}{1024} = \frac{366291}{64000}$$
Gaussian elimination
Given the system of equations
$$16 x + 32 y - \frac{212479}{1000} = 0$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We give the system of equations to the canonical form
$$16 x + 32 y = \frac{212479}{1000}$$
$$32 x + 128 y = \frac{791249}{1000}$$
Rewrite the system of linear equations as the matrix form
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\\32 & 128 & \frac{791249}{1000}\end{matrix}\right]$$
In 1 -th column
$$\left[\begin{matrix}16\\32\end{matrix}\right]$$
let’s convert all the elements, except
1 -th element into zero.
- To do this, let’s take 1 -th line
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\end{matrix}\right]$$
,
and subtract it from other lines:
From 2 -th line. Let’s subtract it from this line:
$$\left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right] = \left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
you get
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\\0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
In 2 -th column
$$\left[\begin{matrix}32\\64\end{matrix}\right]$$
let’s convert all the elements, except
2 -th element into zero.
- To do this, let’s take 2 -th line
$$\left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
,
and subtract it from other lines:
From 1 -th line. Let’s subtract it from this line:
$$\left[\begin{matrix}16 & 0 & \frac{58667}{2000}\end{matrix}\right] = \left[\begin{matrix}16 & 0 & \frac{58667}{2000}\end{matrix}\right]$$
you get
$$\left[\begin{matrix}16 & 0 & \frac{58667}{2000}\\0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
Everything is almost ready - it remains only to find the unknowns by solving elementary equations:
$$16 x_{1} - \frac{58667}{2000} = 0$$
$$64 x_{2} - \frac{366291}{1000} = 0$$
We get the answer:
$$x_{1} = \frac{58667}{32000}$$
$$x_{2} = \frac{366291}{64000}$$
$$16 x + 32 y - \frac{212479}{1000} = 0$$
$$32 x + 128 y - \frac{791249}{1000} = 0$$
We give the system of equations to the canonical form
$$16 x + 32 y = \frac{212479}{1000}$$
$$32 x + 128 y = \frac{791249}{1000}$$
Rewrite the system of linear equations as the matrix form
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\\32 & 128 & \frac{791249}{1000}\end{matrix}\right]$$
In 1 -th column
$$\left[\begin{matrix}16\\32\end{matrix}\right]$$
let’s convert all the elements, except
1 -th element into zero.
- To do this, let’s take 1 -th line
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\end{matrix}\right]$$
,
and subtract it from other lines:
From 2 -th line. Let’s subtract it from this line:
$$\left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right] = \left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
you get
$$\left[\begin{matrix}16 & 32 & \frac{212479}{1000}\\0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
In 2 -th column
$$\left[\begin{matrix}32\\64\end{matrix}\right]$$
let’s convert all the elements, except
2 -th element into zero.
- To do this, let’s take 2 -th line
$$\left[\begin{matrix}0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
,
and subtract it from other lines:
From 1 -th line. Let’s subtract it from this line:
$$\left[\begin{matrix}16 & 0 & \frac{58667}{2000}\end{matrix}\right] = \left[\begin{matrix}16 & 0 & \frac{58667}{2000}\end{matrix}\right]$$
you get
$$\left[\begin{matrix}16 & 0 & \frac{58667}{2000}\\0 & 64 & \frac{366291}{1000}\end{matrix}\right]$$
Everything is almost ready - it remains only to find the unknowns by solving elementary equations:
$$16 x_{1} - \frac{58667}{2000} = 0$$
$$64 x_{2} - \frac{366291}{1000} = 0$$
We get the answer:
$$x_{1} = \frac{58667}{32000}$$
$$x_{2} = \frac{366291}{64000}$$
The graph
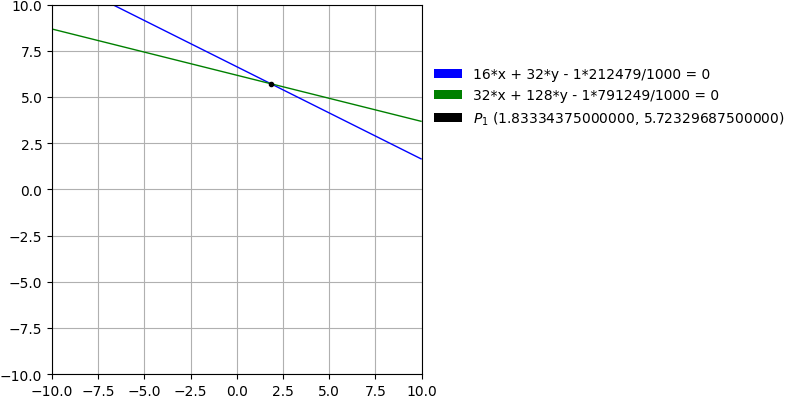

![Solve the system of equations 16x+32y-212,479=0; 32x+128y-791,249=0 (16x plus 32y minus 212,479 equally 0; 32x plus 128y minus 791,249 equally 0) several equations [THERE'S THE ANSWER!] 16x+32y-212,479=0; 32x+128y-791,249=0](/media/krcore-image-pods/176/hash/systemofeqs/e/c4/b108cd1f66758f960bdde7b5e5be4.png)
 16x+32y-212,479=0; 32x+128y-791,249=0
16x+32y-212,479=0; 32x+128y-791,249=0