Mister Exam

Lang:

Other calculators

How to use it?
Sum of series:
(-1)^n
log(1+1/n)
z^(n+1)/factorial(n+1)
log((k+1)/(k+2))
Identical expressions
z^(n+ one)/factorial(n+ one)
z to the power of (n plus 1) divide by factorial(n plus 1)
z to the power of (n plus one) divide by factorial(n plus one)
z(n+1)/factorial(n+1)
zn+1/factorialn+1
z^n+1/factorialn+1
z^(n+1) divide by factorial(n+1)
Similar expressions
z^(n+1)/factorial(n-1)
z^(n-1)/factorial(n+1)

Sum of series/ z^(n+1)/factorial(n+1)

Sum of series z^(n+1)/factorial(n+1)

The solution

You have entered [src]

  oo          
____          
\   `         
 \      n + 1 
  \    z      
  /   --------
 /    (n + 1)!
/___,         
n = 1

$$\sum_{n=1}^{\infty} \frac{z^{n + 1}}{\left(n + 1\right)!}$$

Sum(z^(n + 1)/factorial(n + 1), (n, 1, oo))

The answer [src]

   /              z\
 2 |-2 - 2*z   2*e |
z *|-------- + ----|
   |    2        2 |
   \   z        z  /
--------------------
         2

$$\frac{z^{2} \left(\frac{- 2 z - 2}{z^{2}} + \frac{2 e^{z}}{z^{2}}\right)}{2}$$

z^2*((-2 - 2*z)/z^2 + 2*exp(z)/z^2)/2

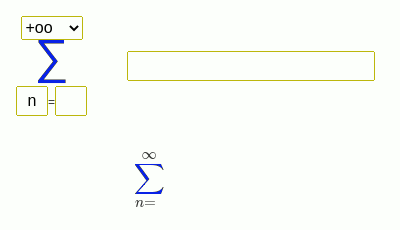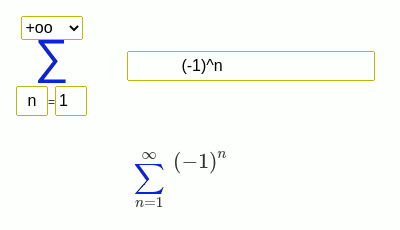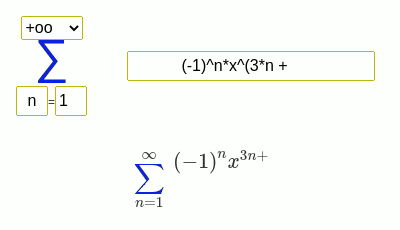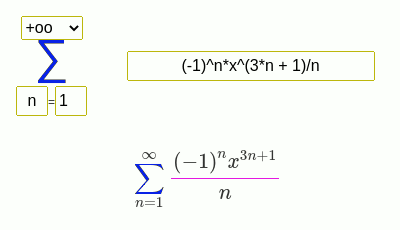
Examples of finding the sum of a series

The Sum of the Power Series
```
x^n/n
```
```
(x-1)^n
```
Factorial
```
1/2^(n!)
```
```
n^2/n!
```
```
x^n/n!
```
```
k!/(n!*(n+k)!)
```
Flint Hills Series
```
csc(n)^2/n^3
```
Basel problem
```
1/n^2
```
```
1/n^4
```
```
1/n^6
```
Harmonic series
```
1/n
```
Grandi's series
```
(-1)^n
```
Alternating series
```
(-1)^(n + 1)/n
```
```
(n + 2)*(-1)^(n - 1)
```
```
(3*n - 1)/(-5)^n
```
```
(-1)^(n - 1)*n/(6*n - 5)
```
Newton–Mercator series
```
(-1)^(n + 1)/n*x^n
```
Exam the series for convergence
```
(3*n - 1)/(-5)^n
```